Il metodo assiomatico¶
La geometria, sin dai tempi di Euclide, è stata organizzata assiomaticamente, partendo cioè dalla fondamenta. Nella matematica queste fondamenta sono costituite dai concetti primitivi e dagli assiomi. Gli enti primitivi sono le nozioni che si decide di non definire. Ci si può rendere facilmente conto, infatti, che non tutto può essere definito, poiché in ogni nozione che si definisce si deve fare ricorso ad altre nozioni, le quali a loro volta devono essere definite per mezzo di altre nozioni e così via all’indietro senza che teoricamente questo processo abbia mai una fine, arrivando necessariamente ad alcune nozioni così primitive da non poter essere definite con altre nozioni più elementari. A queste nozioni non è né necessario né possibile associare alcun significato esplicito, è invece fondamentale esprimere le loro proprietà esclusivamente attraverso assiomi, cioè attraverso proprietà non dimostrabili che indicano però come gli enti primitivi devono e possono essere usati. Il matematico Hilbert utilizza tre enti primitivi - punto, linea e piano - e 21 assiomi. A partire dagli enti primitivi si danno e fanno derivare tutte le definizioni degli enti geometrici.
Nozioni di logica¶
Assumiamo come “primitivo” il concetto base di proposizione (o “giudizio” secondo la terminologia del grande filosofo greco Aristotele): chiamiamo proposizione una frase (affermativa o negativa) a cui abbia senso associare un valore di verità (V, vero, oppure F, falso).
Per esempio, sono proposizioni logiche affermazioni del tipo “Una retta ha infiniti punti”, “2+3=10”. Non sono proposizioni logiche le frasi “1000 è un numero grande”, “il quadrato è semplice”. La prima frase esprime un’affermazione vera, la seconda un’affermazione falsa, la terza e la quarta esprimono affermazioni non valutabili oggettivamente, di queste ultime non si può dire se sono vere o false.
Bisogna tenere conto che una proposizione può essere logica in un sistema e non esserlo in un altro. La possibilità di determinare la verità di una proposizione dipende infatti dalle modalità attraverso cui si può arrivare a determinarne la verità. Per esempio la proposizione “Questo bullone è grande” in generale non è una proposizione logica ma se sappiamo che il metro di riferimento è un determinato dado allora acquisisce una valore logico perché si può stabilire se quel bullone è troppo grande o no. Quindi in generale potremmo dire che una proposizione è decidibile se nel sistema di riferimento esiste un modo per determinarne la veridicità.
La logica delle proposizioni si fonda sui seguenti tre principi della logica aristotelica:
- Il* principio di identità*: ogni oggetto è identico a se stesso e a nessun altro oggetto;
- Il principio di non contraddizione: una stessa proposizione non può essere contemporaneamente vera e falsa;
- Il principio del terzo escluso (“tertium non datur”): una proposizione può essere solo vera o falsa, non può assumere un diverso valore di verità.
Il corpo della geometria, come di qualunque altra teoria matematica, è costituito da proposizioni, cioè da affermazioni che riguardano gli enti geometrici e che sono vere o false.
Le proposizioni possono essere semplici affermazioni (proposizioni atomiche) oppure possono essere ottenute da una o più proposizioni elementari legate tra di loro attraverso connettivi logici (elementi linguistici del tipo “non”, “e”, “oppure”, “o … o”, “quindi”, “se … allora”, “se e solo se”). In questo caso si parla di proposizioni composte o molecolari
Per esempio, la proposizione “un triangolo ha tre lati e ha tre angoli” è composta dalle proposizioni “un triangolo ha tre lati” e “un triangolo ha tre angoli” unite dal connettivo “e”.
| p | q | 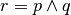 |
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | F |
| p | q | 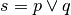 |
| V | V | V |
| V | F | V |
| F | V | V |
| F | F | F |
La congiunzione di due proposizioni si ottiene con il connettivo “e”
(et, and,
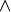 ): la proposizione r ottenuta dalla congiunzione delle proposizioni p e
q, in simboli si usa scrivere
): la proposizione r ottenuta dalla congiunzione delle proposizioni p e
q, in simboli si usa scrivere
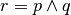 , è vera se entrambe le proposizioni p e q sono contestualmente vere, è
falsa quando anche una sola delle due
proposizioni è falsa.
, è vera se entrambe le proposizioni p e q sono contestualmente vere, è
falsa quando anche una sola delle due
proposizioni è falsa.
Per esempio, “Ho avuto 7 in italiano e matematica” è un’affermazione vera solo quando ho avuto 7 in entrambe le materie.
Per esprimere tutte le possibilità in maniera sintetica si usa una tabella a doppia entrata, detta tavola di verità.
La disgiunzione (inclusiva) di due proposizioni si ottiene con il
connettivo “o” (vel, or,
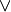 ): la proposizione s ottenuta dalla disgiunzione di due proposizioni p e
q, in simboli
): la proposizione s ottenuta dalla disgiunzione di due proposizioni p e
q, in simboli
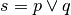 , è vera quando almeno una delle due proposizioni è vera, è falsa solo se
entrambe le proposizioni sono false.
, è vera quando almeno una delle due proposizioni è vera, è falsa solo se
entrambe le proposizioni sono false.
| p | q | 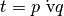 |
| V | V | F |
| V | F | V |
| F | V | V |
| F | F | F |
La disgiunzioneesclusiva di due proposizioni si ottiene con il connettivo [o
congiunzione] “o … o”
(aut, xor,
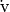 ): la proposizione t ottenuta dalla disgiunzione esclusiva di due proposizioni
p e q, in simboli
): la proposizione t ottenuta dalla disgiunzione esclusiva di due proposizioni
p e q, in simboli
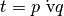 , è vera quando solo una delle due proposizioni è vera, è falsa quando le due
proposizioni sono entrambe vere o entrambe false.
, è vera quando solo una delle due proposizioni è vera, è falsa quando le due
proposizioni sono entrambe vere o entrambe false.
Per esempio, nell’affermazione “Oggi il Milan vince o pareggia” la congiunzione “o” ha valore esclusivo.
Esempio
p=”un triangolo ha tre lati” (Vera).. tabq=”un triangolo ha tre vertici” (Vera)
r=”un triangolo ha quattro angoli” (Falsa).. tabs=”un triangolo ha tre dimensioni” (Falsa)
Allora
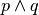 è vera,
è vera,
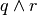 è falsa,
è falsa,
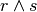 è falsa.
è falsa.
Inoltre
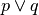 è vera,
è vera,
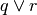 è vera,
è vera,
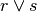 è falsa.
è falsa.
Invece
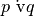 è falsa,
è falsa,
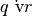 è vera,
è vera,
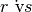 è falsa.
è falsa.
La negazione (connettivo “non”, simboli non, not,
 ) è un operatore che, a differenza dei precedenti, non lega più proposizioni
ma agisce su un’unica proposizione (per questo si dice che è un operatore
unario, in analogia all’operazione insiemistica di complementazione). La
negazione di una proposizione p è una proposizione che si indica con il
simbolo
) è un operatore che, a differenza dei precedenti, non lega più proposizioni
ma agisce su un’unica proposizione (per questo si dice che è un operatore
unario, in analogia all’operazione insiemistica di complementazione). La
negazione di una proposizione p è una proposizione che si indica con il
simbolo
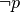 che è vera se p è falsa, viceversa è falsa se p è vera.
che è vera se p è falsa, viceversa è falsa se p è vera.
La doppia negazione equivale ad un’affermazione, cioè
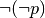 è equivalente a
è equivalente a
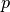 .
.
La tavola di verità è la seguente:
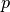 |
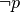 |
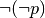 |
| V | F | V |
| F | V | F |
Esempio
- In riferimento agli esempi precedenti,
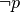 e
e
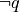 sono false, mentre
sono false, mentre
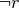 e
e
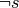 sono vere.
sono vere.
È piuttosto semplice capire il meccanismo della negazione se applicata a proposizioni atomiche, spesso è meno intuitivo il valore di verità della negazione di una proposizione più complessa.
Ad esempio, la negazione
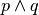 di non è
di non è
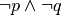 bensì
bensì
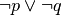 , mentre la negazione di
, mentre la negazione di
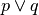 è
è
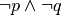 e non
e non
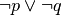 .
.
In formule:
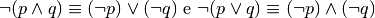 .
.
Per esempio, “Non è vero che Marco e Luca sono stati bocciati” può voler dire che entrambi non sono stati bocciati o solo uno di loro non è stato bocciato.
Queste uguaglianze prendono il nome di leggi di De Morgan.
La verifica si può vedere dalla seguente tavola di verità:
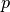 |
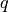 |
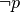 |
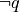 |
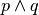 |
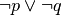 |
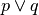 |
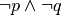 |
| V | V | F | F | V | F | V | F |
| V | F | F | V | F | V | V | F |
| F | V | V | F | F | V | V | F |
| F | F | V | V | F | V | F | V |
Come per le operazioni aritmetiche anche per gli operatori logici è possibile analizzarne le proprietà. Ne indichiamo qualcuna a titolo di esempio:
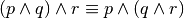 .. tabproprietà associativa della congiunzione
.. tabproprietà associativa della congiunzione
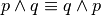 .. tabproprietà commutativa della congiunzione
.. tabproprietà commutativa della congiunzione
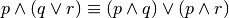 .. tabproprietà distributiva della congiunzione rispetto alla disgiunzione
.. tabproprietà distributiva della congiunzione rispetto alla disgiunzione
Predicati e quantificatori¶
Una proposizione che fa riferimento a una proprietà o caratteristica di alcuni elementi di un insieme si chiama predicato. Le frasi formate da un predicato che ha alcuni argomenti incogniti si dicono enunciati aperti.
Per esempio, p = “x è un numero intero maggiore di 10” è un enunciato aperto.
Consideriamo ora le seguenti affermazioni:
- “Tutti gli uomini sono mortali” si riferisce a un qualsiasi essere umano;
- “Tutti i multipli di 6 sono anche multipli di 2” è vera per tutti i numeri multipli di 6;
- “Ogni numero negativo è minore di ogni numero positivo”.
I predicati precedenti non riguardano un elemento specifico ma una certa
quantità di elementi. I termini “tutti” e “ogni”, detti quantificatori
universali, indicano che una proprietà è vera per tutti gli elementi di un
certo
insieme. In logica matematica si usa il simbolo
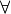 , leggi “per ogni”, per indicare il quantificatore universale.
, leggi “per ogni”, per indicare il quantificatore universale.
Vediamo ora i seguenti predicati:
- “Esiste un numero che elevato al quadrato dà 16”
- “Alcuni numeri pari sono anche multipli di 3.”
Queste affermazioni esprimono proprietà che sono vere almeno per un elemento dell’insieme di riferimento: la prima frase è vera per i numeri +4 e -4, la seconda frase è vera per i numeri 6, 12, 18, …
I termini “c’è almeno”, “alcuni”, “esiste almeno uno” si dicono
quantificatori esistenziali e si indicano con il simbolo
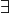 , leggi “esiste”.
, leggi “esiste”.
Bisogna prestare particolare attenzione quando si negano frasi in cui compaiono i quantificatori. Per esempio la negazione di “Tutti i gatti fanno le fusa” non è “Nessun gatto fa le fusa” bensì “Non tutti i gatti fanno le fusa” che si può esprimere anche con il quantificatore esistenziale “c’è almeno un gatto che non fa le fusa”.
La negazione della frase “L’anno scorso siamo stati tutti promossi” non è “L’anno scorso siamo stati tutti bocciati” ma “L’anno scorso c’è stato almeno uno di noi che non è stato promosso”.
Esempio
- Se si considera la proposizione p = “Tutti i quadrati hanno due
diagonali”, la sua negazione è la proposizione
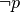 = “Non tutti i quadrati hanno due diagonali”.
= “Non tutti i quadrati hanno due diagonali”.
Il linguaggio comune ci indurrebbe a considerare come negazione di p la proposizione “Nessun quadrato ha due diagonali”, in realtà per avere la negazione della proposizione p basta che esista almeno un quadrato che non ha due diagonali.
L’implicazione¶
Nel linguaggio matematico sono comuni proposizioni del tipo “Se p allora q”. Ad esempio “Se un numero è multiplo di 12 allora è multiplo di 3”. La frase precedente può essere espressa dicendo:
“Essere multiplo di 12 implica essere multiplo di 3”.
In logica frasi del tipo “Se p allora q” vengono tradotte utilizzando
l’operatore infisso (ovvero interposto fra le proposizioni)
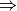 detto implicazione.
detto implicazione.
La scrittura “se p allora q” si traduce con la scrittura
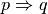 , che si legge “p implica q”.
, che si legge “p implica q”.
La proposizione p è detta antecedente, (o ipotesi) la proposizione B è detta conseguente (o tesi).
Il significato logico della proposizione
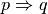 è che “tutte le volte che la proposizione p è vera allora risulta vera
anche la proposizione q”. Ovvero non si dà il caso che p sia vera e q sia
falsa.
è che “tutte le volte che la proposizione p è vera allora risulta vera
anche la proposizione q”. Ovvero non si dà il caso che p sia vera e q sia
falsa.
Per esempio, l’affermazione “Se c’è il sole andiamo al mare” è falsa solo quando c’è il sole e non andiamo al mare; l’affermazione, infatti, non dice nulla se il sole non c’è: quindi se non c’è il sole si è liberi di andare o non andare al mare. Anche l’affermazione “Se studi sarai promosso” dice solo che se studi dovrai essere promosso, non dice nulla per il caso in cui tu non studi, in questo caso infatti potrai essere ugualmente promosso.
La tavola di verità è la seguente:
| p | q | 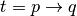 |
| V | V | V |
| V | F | F |
| F | V | V |
| F | F | V |
Uno degli errori logici più comuni è quello di pensare che da
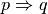 si possa dedurre
si possa dedurre
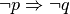 .
.
Ad esempio dall’affermazione “Se piove prendo l’ombrello” qualcuno può pensare che si possa dedurre “Se non piove non prendo l’ombrello”. Tuttavia, riflettendoci si intuisce che le due frasi non sono affatto consequenziali. Basta pensare che chi pronuncia la prima frase sta affermando che tutte le volte che piove prende naturalmente l’ombrello, ma non esclude la possibilità di prenderlo anche quando non piove (in effetti è saggio farlo se il cielo è coperto da nuvoloni neri!).
Così la frase:.. taba) “Se x è multiplo di 12 allora è multiplo di 3”
non vuol dire:.. tabb) “Se x non è multiplo di 12 allora non è multiplo di 3”
Infatti la (a) è vera, mentre la (b) è falsa (si pensi al 6 che non è multiplo di 12 ma è multiplo di 3).
Ciò che ragionevolmente si può dedurre da
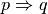 è
è
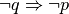 .
.
Ad esempio da:
“Se x è multiplo di 12 allora è multiplo di 3”
si può dedurre:
“Se x non è multiplo di 3 allora non è multiplo di 12”
Data l’implicazione
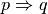 la proposizione p viene detta condizione sufficiente per q. Mentre la
proposizione q viene detta** condizione necessaria** per p.
la proposizione p viene detta condizione sufficiente per q. Mentre la
proposizione q viene detta** condizione necessaria** per p.
Per esempio, studiare è condizione necessaria per essere promossi ma non è sufficiente.
Quest’ultima espressione fa appunto riferimento al fatto che da
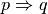 si può dedurre
si può dedurre
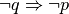 . Ossia q è necessaria per p in quanto se non è vera q non è vera neanche p.
. Ossia q è necessaria per p in quanto se non è vera q non è vera neanche p.
Calcoliamo la tavola di verità di
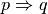 e di
e di
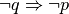
| p | q | 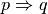 |
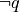 |
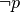 |
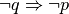 |
|
| V | V | V | F | F | V | |
| V | F | F | V | F | F | |
| F | V | V | F | V | V | |
| F | F | V | V | V | V |
Come si vede, le due proposizioni hanno gli stessi valori di verità.
In generale, data un’implicazione
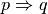 (proposizione diretta):
(proposizione diretta):
- l’implicazione
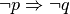 si dice contraria di
si dice contraria di
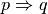 ;
; - l’implicazione
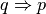 si dice inversa di
si dice inversa di
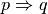 ;
; - l’implicazione
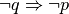 si dice contronominale (o controinversa) di
si dice contronominale (o controinversa) di
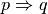 .
.
La doppia implicazione, o equivalenza logica, di due proposizioni p e q
dà luogo a una proposizione che in simboli si
rappresenta
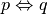 (leggasi “p se e solo se q”) che è vera se p e q sono entrambe vere o
entrambe false. La tavola di verità è la seguente:
(leggasi “p se e solo se q”) che è vera se p e q sono entrambe vere o
entrambe false. La tavola di verità è la seguente:
| p | q | 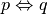 |
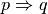 |
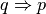 |
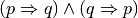 |
|
| V | V | V | V | V | V | |
| V | F | F | F | V | F | |
| F | V | F | V | F | F | |
| F | F | V | V | V | V |
L’operatore
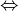 è detto di doppia implicazione perché se vale
è detto di doppia implicazione perché se vale
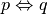 allora valgono anche
allora valgono anche
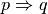 e
e
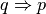 , e viceversa. Nella tabella precedente, infatti, è stata messa in evidenza
l’equivalenza logica tra la proposizione
, e viceversa. Nella tabella precedente, infatti, è stata messa in evidenza
l’equivalenza logica tra la proposizione
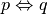 e la proposizione
e la proposizione
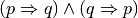 .
.
L’equivalenza logica è un relazione di equivalenza, infatti verifica le seguenti proprietà
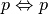 .. tabriflessiva
.. tabriflessiva- se
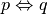 allora vale anche
allora vale anche
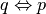 .. tabsimmetrica
.. tabsimmetrica - se
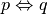 e
e
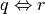 allora vale anche
allora vale anche
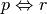 .. tabtransitiva.
.. tabtransitiva.
In matematica si usa spesso l’espressione “p è condizione necessaria e
sufficiente per q”. Per esempio “Condizione necessaria e sufficiente
affinché un
numero sia divisibile per 3 è che la somma delle sue cifre sia divisibile per
3”. Il significato della frase è che “p è sufficiente
per q” e inoltre “p è necessario per q”. In altre parole significa dire
che
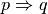 e .
e .
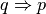 Nel caso dell’esempio, “se un numero è divisibile per 3 allora la somma
delle sue cifre è divisibile per 3” e vale anche l’implicazione inversa
“se la somma delle cifre di un numero è divisibile per 3 allora il numero
stesso è divisibile per 3”.
Nel caso dell’esempio, “se un numero è divisibile per 3 allora la somma
delle sue cifre è divisibile per 3” e vale anche l’implicazione inversa
“se la somma delle cifre di un numero è divisibile per 3 allora il numero
stesso è divisibile per 3”.
I teoremi¶
Un teorema è una proposizione composta del tipo
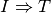 , cioè una implicazione tra due proposizioni, dette Ipotesi e Tesi. Dimostrare
un teorema significa fare un ragionamento che permetta di concludere che la Tesi
è vera avendo supposto che l’Ipotesi è vera. Nel caso in cui un teorema sia
dimostrabile all’interno di una teoria, si dice che è un teorema valido. In
riferimento alla terminologia usata quando abbiamo parlato dell’implicazione,
chiamiamo
, cioè una implicazione tra due proposizioni, dette Ipotesi e Tesi. Dimostrare
un teorema significa fare un ragionamento che permetta di concludere che la Tesi
è vera avendo supposto che l’Ipotesi è vera. Nel caso in cui un teorema sia
dimostrabile all’interno di una teoria, si dice che è un teorema valido. In
riferimento alla terminologia usata quando abbiamo parlato dell’implicazione,
chiamiamo
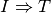 “teorema diretto”,
“teorema diretto”,
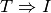 “teorema inverso”,
“teorema inverso”,
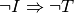 “teorema contrario”,
“teorema contrario”,
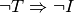 “teorema controinverso”, e ribadiamo l’equivalenza tra il teorema diretto
ed il teorema contro inverso, nonché l’equivalenza tra il teorema contrario
ed il teorema inverso, mentre in generale la validità del teorema diretto non
implica la validità del teorema inverso, e viceversa. Nel caso particolare in
cui vale sia
“teorema controinverso”, e ribadiamo l’equivalenza tra il teorema diretto
ed il teorema contro inverso, nonché l’equivalenza tra il teorema contrario
ed il teorema inverso, mentre in generale la validità del teorema diretto non
implica la validità del teorema inverso, e viceversa. Nel caso particolare in
cui vale sia
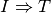 sia
sia
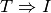 , si scrive
, si scrive
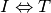 e si dice che Ipotesi e Tesi sono logicamente equivalenti. Più
precisamente, nel linguaggio specifico delle scienze che fanno uso della
logica, e quindi anche nel linguaggio della Geometria Razionale, se vale
e si dice che Ipotesi e Tesi sono logicamente equivalenti. Più
precisamente, nel linguaggio specifico delle scienze che fanno uso della
logica, e quindi anche nel linguaggio della Geometria Razionale, se vale
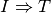 , si dice che “I è condizione sufficiente per T” e anche che “T è
condizione necessaria per I”; se in particolare vale
, si dice che “I è condizione sufficiente per T” e anche che “T è
condizione necessaria per I”; se in particolare vale
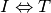 , si usa dire che “I è condizione necessaria e sufficiente per T”.
, si usa dire che “I è condizione necessaria e sufficiente per T”.
In generale incontreremo molti teoremi che vengono denominati genericamente “proposizioni”, perché il nome di “Teorema” viene tradizionalmente attribuito solo ai teoremi più importanti. Inoltre si usa chiamare “lemma” una proposizione che non ha una grande importanza di per sé, ma che è particolarmente utile per la dimostrazione di altri teoremi. Si chiama invece “corollario” un teorema importante che è una conseguenza immediata di un altro teorema.
Così come abbiamo visto che non è possibile definire tutto e che quindi bisogna assumere alcune nozioni come primitive, analogamente non è possibile dimostrare tutte le proposizioni di una teoria. Alcune proposizioni devono essere assunte come vere e costituiscono la base della dimostrazione dei teoremi; queste proposizioni si chiamano “postulati” o “assiomi”. Risulta evidente che cambiando sia pure uno solo degli assiomi cambiano anche i teoremi dimostrabili e quindi la teoria.
In generale, come abbiamo detto, dato un teorema (diretto) del tipo
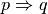 , la sua validità non garantisce la validità del teorema (inverso)
, la sua validità non garantisce la validità del teorema (inverso)
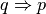 . Questo però può succedere. In ogni caso, se sono vere
. Questo però può succedere. In ogni caso, se sono vere
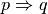 e
e
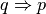 , le due proposizioni sono logicamente equivalenti, ossia
, le due proposizioni sono logicamente equivalenti, ossia
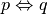 .
.
Esempio
- Teorema: un triangolo che ha i lati uguali ha anche gli angoli uguali.
Il teorema si può schematizzare nel seguente modo: p = ”un triangolo ha i
lati uguali”; q = ”un triangolo ha gli angoli uguali”. Il teorema
enunciato è
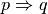 . Il teorema inverso è
. Il teorema inverso è
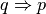 , cioè:
, cioè:
- Teorema inverso: un triangolo che ha gli angoli uguali ha anche i lati uguali.
In tale esempio sono validi sia il teorema diretto sia il teorema inverso. Il fatto che uno dei due teoremi sia chiamato diretto e l’altro inverso è un fatto soggettivo, che può dipendere semplicemente dall’ordine con cui si enunciano i teoremi.
Il teorema precedente si può esporre allora nel seguente modo.
- Teorema: un triangolo ha i lati uguali se e solo se ha gli angoli uguali.
La deduzione¶
Nel paragrafo precedente abbiamo parlato in modo generico di implicazione,
deduzione, dimostrazione. Facciamo ora attenzione alla differenza tra
implicazione materiale e deduzione logica. L’implicazione è
un’operazione tra proposizioni, mentre la deduzione è il ragionamento che
costituisce la base della dimostrazione di un teorema.
Per l’implicazione materiale si usa il simbolo
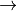 mentre per la deduzione logica si usa il simbolo
mentre per la deduzione logica si usa il simbolo
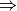 .
.
La frase “Se 5 è un numero pari, allora il triangolo ha 4 lati” è
perfettamente valida ed anzi è vera, poiché la premessa (proposizione
antecedente) è falsa, per cui l’implicazione è vera anche se la proposizione
conseguente è falsa (si tenga presente la tavola di verità di
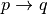 ).
).
Si noti però che la definizione di implicazione ha senso solamente se la
premessa è vera, il suo ampliamento al caso in cui la premessa è falsa è
motivata da ragioni di completezza della trattazione. Bisogna quindi fare
attenzione ad usare l’implicazione logica quando la premessa è falsa. Teniamo
comunque conto che se p è falsa allora
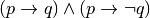 cioè
cioè
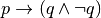 è vera. Ma
è vera. Ma
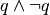 è una contraddizione, quindi una premessa falsa implica sempre una
contraddizione.
è una contraddizione, quindi una premessa falsa implica sempre una
contraddizione.
In realtà, la dimostrazione di un teorema non è la verifica della validità dell’implicazione, anzi è un procedimento che fa uso della validità dell’implicazione stessa. In un teorema si parte dal supporre vera l’ipotesi e si dimostra, mediante gli assiomi ed altri teoremi già dimostrati in precedenza, che anche la tesi è vera (questo se si vuole seguire il procedimento diretto). Se si vuole seguire il procedimento indiretto (o per assurdo), si suppone che la tesi sia falsa e, sempre mediante assiomi e altri teoremi già dimostrati, si arriva ad affermare che l’ipotesi è falsa (cosa che non si deve accettare).
Le principali regole del corretto ragionamento seguono alcuni schemi particolari (detti sillogismi, dal nome attribuito ad essi da Aristotele). Presentiamo qui i quattro principali sillogismi: il modus ponens, il modus tollens, il sillogismo disgiuntivo, il sillogismo ipotetico.
| ponens | tollens | disgiuntivo | ipotetico | ||||||
| 2a premessa | 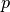 |
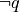 |
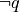 |
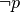 |
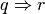 |
||||
| conclusione | 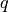 |
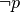 |
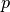 |
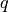 |
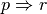 |
||||
Suggeriamo una lettura degli schemi appena esposti:
- modus ponens: “se sappiamo che p implica q, e sappiamo che p è vera, allora possiamo concludere che anche q è vera” (metodo diretto di dimostrazione);
- modus tollens: “se sappiamo che p implica q, e sappiamo che q è falsa, allora possiamo concludere che anche p è falsa” (metodo indiretto di dimostrazione);
- sillogismo disgiuntivo: “se sappiamo che, tra p e q, almeno una delle due è vera, e sappiamo che q (rispettivamente p) è falsa, allora possiamo concludere che p (rispettivamente q) è vera”;
- sillogismo ipotetico: “se sappiamo che p implica q, e sappiamo che q implica r, allora possiamo concludere che p implica r” (proprietà transitiva dell’implicazione).
Altre regole (note come i Giudizi di Aristotele) fanno uso dei predicati e
dei quantificatori, per cui
riprendiamo l’Esempio 3 e vediamo di tradurre la frase “Tutti i quadrati
hanno due diagonali” e la
sua negazione “Non tutti i quadrati hanno due diagonali” in formule che
fanno uso anche del linguaggio degli insiemi. Se chiamiamo Q l’insieme di
tutti i quadrati, e chiamiamo P la proprietà dell’avere due diagonali, se x
è il generico quadrato (elemento di Q), P(x) è il predicato “x gode della
proprietà P”, cioè “x ha due diagonali”, la frase “Tutti i quadrati
hanno due diagonali” si traduce così in simboli:
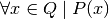 .
.
La sua negazione è: “Esiste almeno un quadrato che non ha due diagonali,
cioè che non gode della proprietà P”, e si traduce in simboli così:
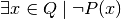 .
.
In quest’ultimo caso, la virgola può anche essere sostituita da una barra verticale (“|”) e si legge “tale che”.
Analogamente, una frase del tipo “Esiste almeno un numero naturale che sia
divisore di 10” può scriversi come:
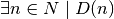 , dove D è la proprietà dell’essere divisore di 10 e D(n) significa che n
verifica la proprietà D, cioè che n è un divisore di 10. La sua negazione è
“Nessun numero naturale è divisore di 10”, ovvero “preso un qualsiasi
numero naturale n, questo non gode della proprietà D” e la traduzione in
simboli di tale frase è:
, dove D è la proprietà dell’essere divisore di 10 e D(n) significa che n
verifica la proprietà D, cioè che n è un divisore di 10. La sua negazione è
“Nessun numero naturale è divisore di 10”, ovvero “preso un qualsiasi
numero naturale n, questo non gode della proprietà D” e la traduzione in
simboli di tale frase è:
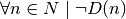 .
.
È il caso di inserire in uno schema queste quattro proposizioni (che corrispondono ai Giudizi di Aristotele):
| affermativo | 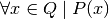 |
affermativo | 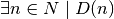 |
| P è vera per ogni x | D è vera per almeno un n | ||
| negativo | 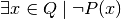 |
negativo | 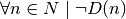 |
| P è falsa per almeno un x | D è falsa per ogni n |
Se chiamiamo R l’insieme degli elementi che verificano la proprietà P, e S l’insieme degli elementi che verificano la proprietà D, i quattro Giudizi si possono rappresentare graficamente nel modo seguente:
La dimostrazione¶
Tenendo conto di quanto detto precedentemente, dimostrare che
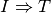 significa fare un ragionamento che permetta di concludere che la tesi T è vera
avendo supposto che l’ipotesi I è vera.
significa fare un ragionamento che permetta di concludere che la tesi T è vera
avendo supposto che l’ipotesi I è vera.
Quando attraverso un ragionamento logico, e cioè attraverso una catena di
implicazioni del tipo
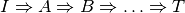 , si riesce a dedurre la verità di una proposizione Ta partire dalla verità di
una proposizione I, si dice che si è data una dimostrazione diretta del
teorema
, si riesce a dedurre la verità di una proposizione Ta partire dalla verità di
una proposizione I, si dice che si è data una dimostrazione diretta del
teorema
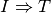 (attraverso le regole del modus ponens e del sillogismo ipotetico). Le
regole da seguire sono state in parte illustrate quando si è parlato di
deduzione.
(attraverso le regole del modus ponens e del sillogismo ipotetico). Le
regole da seguire sono state in parte illustrate quando si è parlato di
deduzione.
Un teorema può anche essere dimostrato per assurdo, o con metodo indiretto, che consiste nel partire dalla negazione di T e, attraverso una catena di implicazioni, arrivare alla negazione di I o, in generale, ad una contraddizione.
Esistono altri metodi di dimostrazione, di cui eventualmente si parlerà più diffusamente qualora si dovesse ricorrere ad essi. Per ora ci limitiamo a citarne un paio: dimostrazione per induzione e dimostrazione mediante esempio o controesempio.
La** dimostrazione per induzione** si usa in particolare quando vogliamo dimostrare una proprietà generale che vale per molte categorie di figure ma che non si può esprimere in maniera unica per tutte le categorie (ad esempio una proprietà che vale per tutti i poligoni ma che dipende dal numero dei lati, come l’estensione dei criteri di congruenza dei triangoli a poligoni di più lati).
Si usa invece un esempio quando bisogna dimostrare che una certa proprietà vale per almeno un oggetto del nostro studio o un controesempio per dimostrare che una proprietà non vale per tutti gli oggetti in esame.
Per fornire alcuni esempi di dimostrazione, avremmo bisogno di fissare prima i concetti di base e gli assiomi da cui partire, per cui rinviamo la questione al prossimo paragrafo.
Ma a cosa serve studiare la dimostrazione di un teorema? Perché non ci limitiamo ad elencare i teoremi? Per molte applicazioni basta in effetti conoscere il teorema e a volte anche soltanto la formula risolutiva. Tuttavia studiando le dimostrazioni si impara a dimostrare e quindi si impara a creare nuova matematica. Un altro importante vantaggio è che la dimostrazione spiega perché il teorema è vero e permette di scoprire la struttura nascosta nelle definizioni e nei teoremi. Quando si studia una dimostrazione non bisogna limitarsi a leggerla e a impararla a memoria, occorre leggerla attivamente, ponendo attenzione su cosa si fa e cercando di anticipare i passaggi. Se un passaggio non è chiaro bisogna prima tornare indietro per capire come ci si è arrivati e poi si cerca di capire il perché l’autore ha messo quel passaggio. In generale, una dimostrazione va letta più volte smettendo solo quando si è compresa a fondo.
Esercizi¶
1.7.1 Nozioni di logica¶
Quali delle seguenti frasi sono proposizioni logiche?
- I matematici sono intelligenti.. tabSìNo
- 12 è un numero dispari.. tabSìNo
- Pascoli è stato un grande poeta.. tabSìNo
- Pascoli ha scritto La Divina Commedia.. tabSìNo
- Pascoli ha scritto poesie.. tabSìNo
- Lucia è una bella ragazza.. tabSìNo
- Lucia ha preso 8 al compito di matematica.. tabSìNo
A partire dalle due proposizioni:p = “16 è divisibile per 2” q = “16 è divisibile per 4”
costruisci le proposizioni
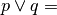
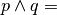
A partire dalle proposizioni:p=”18 è divisibile per 3” q=”18 è numero dispari”
costruisci le proposizioni di seguito indicate e stabilisci il loro valore di verità
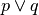 .. tabV F
.. tabV F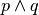 .. tabV F
.. tabV F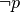 .. tabV F
.. tabV F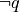 .. tabV F
.. tabV F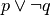 .. tabV F
.. tabV F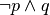 .. tabV F
.. tabV F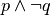 .. tabV F
.. tabV F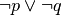 .. tabV F
.. tabV F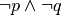 .. tabV F
.. tabV F
In quale delle seguenti proposizioni si deve usare la o inclusiva e in quali la o esclusiva:
- Nelle fermate a richiesta l’autobus si ferma se qualche persona deve scendere o salire.
- Luca sposerà Maria o Claudia.
- Fammi chiamare da Laura o da Elisa.
- Si raggiunge l’unanimità quando sono tutti favorevoli o tutti contrari.
La disgiunzione esclusiva
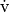 a volte non viene messa tra gli operatori logici fondamentali perché è
esprimibile attraverso gli altri tre altri operatori presentati finora.
a volte non viene messa tra gli operatori logici fondamentali perché è
esprimibile attraverso gli altri tre altri operatori presentati finora.Verificare che date due proposizioni p e q, la proposizione composta
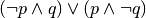 è equivalente alla proposizione
è equivalente alla proposizione
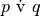 . Dimostrare poi l’equivalenza usando le tavole della verità.
. Dimostrare poi l’equivalenza usando le tavole della verità.A partire dalla preposizioni:p = ”Oggi pioverà”
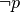 = ”Oggi non pioverà”
= ”Oggi non pioverà”scrivere le preposizioni
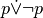 ,
,
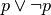 ,
,
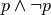 . Scrivere quindi la loro tabella della verità.
. Scrivere quindi la loro tabella della verità.Scrivere le tabelle di verità delle formule
a)
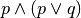 .. tabb)
.. tabb)
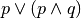 .. tabc)
.. tabc)
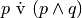
d)
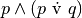 .. tabe)
.. tabe)
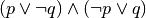 .. tabf)
.. tabf)
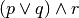
Qual è la negazione della frase “Ogni volta che ho preso l’ombrello non è piovuto”?
- [ ] Almeno una volta sono uscito con l’ombrello ed è piovuto
- [ ] Quando esco senza ombrello piove sempre
- [ ] Tutti i giorni in cui non piove esco con l’ombrello
- [ ] Tutti i giorni che è piovuto ho preso l’ombrello
Una proposizione che è sempre vera indipendentemente dalla verità degli elementi che lo compongono è detta tautologia. Una proposizione che è sempre falsa indipendentemente dalla verità dei suoi elementi è invece della contraddizione.
La proposizione composta
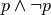 è una contraddizione in quanto è sempre falsa.
è una contraddizione in quanto è sempre falsa.La proposizione composta
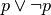 è una tautologia in quanto è sempre vera.
è una tautologia in quanto è sempre vera.Costruisci le tavole di verità per le proposizioni composte
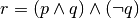 .. tab
.. tab
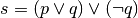
Cosa puoi dire delle proposizioni r ed s?
1.7.2. Predicati e quantificatori¶
- Scrivi le negazioni delle seguenti frasi che contengono dei quantificatori
- Al compito di matematica eravamo tutti presenti.
- Ogni giorno il professore ci dà sempre compiti per casa.
- Ogni giorno Luca vede il telegiornale.
- Tutti i miei familiari portano gli occhiali.
- Tutti hanno portato i soldi per la gita.
- Sono date le frasi p = ”Mario è cittadino romano”, q = ”Mario è cittadino italiano”, scrivi per esteso le seguenti implicazioni e indica quale di esse è vera.
a)
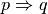 .. tabV.. tabF.. tabb)
.. tabV.. tabF.. tabb)
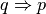 .. tabV.. tabF.. tabc)
.. tabV.. tabF.. tabc)
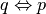 .. tabV.. tabF
.. tabV.. tabF
- Trasforma nella forma “Se… allora…” le seguenti frasi:
- Un oggetto lanciato verso l’alto ricade a terra.
- Quando piove prendo l’ombrello.
- I numeri la cui ultima cifra è 0 sono divisibili per 5.
- Per essere promosso occorre aver raggiunto la sufficienza.
- Date le proposizioni p e q costruire la tavola di verità di
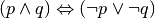 .
.
1.7.3 Teoremi¶
- Scrivere la contronominale di “Tutti gli alunni che hanno avuto il debito in matematica hanno avuto almeno due valutazioni insufficienti in matematica”.
- Completa i seguenti ragionamenti:
- Se un numero è multiplo di 10 allora è pari; il numero n non è pari quindi … … … ………
- Se il sole tramonta fa buio; il sole è tramontato quindi … … … … … … … … … … … …
- Dimostra con un controesempio che non è vera l’affermazione “Tutti i multipli di 3 sono dispari”.
- Nel teorema “Il quadrato è anche rettangolo” esplicitare l’ipotesi e la ‘tesi’. Enunciare il teorema contrario. Trova un contro esempio che dimostra che il teorema contrario è falso.
- Dimostra per assurdo il teorema “Se un numero non è divisibile per 2 allora non è divisibile per 10”.
- Ecco le dichiarazioni rilasciate da quattro amiche: Anna: “Io sono la più anziana”; Carla: “Io non sono né la più giovane né la più anziana”; Liliana: “Io non sono la più giovane”; Milena: “Io sono la più giovane”. Il fatto è che una di loro (e solo una) ha mentito. Chi è, delle quattro amiche, effettivamente la più giovane?(Giochi d’autunno, 2010)
- Dopo una rissa in campo l’arbitro vuole espellere il capitano di una squadra
di calcio. E’ uno tra Paolo, Andrea e Gabriele ma, siccome nessuno ha la
fascia al braccio, non sa qual è dei tre. Paolo dice di non essere il
capitano; Andrea dice che il capitano è Gabriele; Gabriele dice che il
capitano è uno degli altri due. Sapendo che uno solo dei tre dice la
verità, quale delle affermazioni seguenti è sicuramente vera?
- [ ] Gabriele non è il capitano,
- [ ] Andrea dice la verità,
- [ ] Paolo dice la verità,
- [ ] Andrea è il capitano,
- [ ] Gabriele mente. (I Giochi di Archimede, 2011)
- Un celebre investigatore sta cercando il colpevole di un omicidio tra cinque sospettati: Anna, Bruno, Cecilia, Dario ed Enrico. Egli sa che il colpevole mente sempre e gli altri dicono sempre la verità. Anna afferma: “Il colpevole è un maschio”, Cecilia dice: “E’ stata Anna oppure è stato Enrico”. Infine Enrico dice: “Se Bruno è colpevole allora Anna è innocente”. Chi ha commesso l’omicidio?(I Giochi di Archimede, 2010)
- Quattro amici, Anna, Bea, Caio e Dino, giocano a poker con 20 carte di uno stesso mazzo: i quattro re, le quattro regine, i quattro fanti, i quattro assi e i quattro dieci. Vengono distribuite cinque carte a testa. Anna dice: “Io ho un poker!” (quattro carte dello stesso valore). Bea dice: “Io ho tutte e cinque le carte di cuori”. Caio dice: “Io ho cinque carte rosse”. Infine Dino dice: “Io ho tre carte di uno stesso valore e anche le altre due hanno lo stesso valore”. Sappiamo che una e una sola delle affermazioni è falsa; chi sta mentendo?(I Giochi di Archimede, 2009)
- Un satellite munito di telecamera inviato sul pianeta Papilla ha permesso di stabilire che è falsa la convinzione di qualcuno che: “su Papilla sono tutti grassi e sporchi”. Quindi adesso sappiamo che: [ ] su Papilla almeno un abitante è magro e pulito, [ ] su Papilla tutti gli abitanti sono magri e puliti, [ ] almeno un abitante di Papilla è magro, [ ] almeno un abitante di Papilla è pulito, [ ] se su Papilla tutti gli abitanti sono sporchi, almeno uno di loro è magro.(I Giochi di Archimede, 2008)
- Anna, Barbara, Chiara e Donatella si sono sfidate in una gara di nuoto fino
alla boa. All’arrivo non ci sono stati ex-equo. Al ritorno, Anna dice:
“Chiara è arrivata prima di Barbara”; Barbara dice: “Chiara è
arrivata prima di Anna”; Chiara dice: “Io sono arrivata seconda”.
Sapendo che una sola di esse ha detto la verità,
- [ ] si può dire solo chi ha vinto,
- [ ] si può dire solo chi è arrivata seconda,
- [ ] si può dire solo chi è arrivata terza,
- [ ] si può dire solo chi è arrivata ultima,
- [ ] non si può stabile la posizione in classifica di nessuna. (I Giochi di Archimede, 2000)
- “In ogni scuola c’è almeno una classe in cui sono tutti promossi”.
Volendo negare questa affermazione, quale dei seguenti enunciati
sceglieresti?
- [ ] In ogni scuola c’è almeno una classe in cui sono tutti bocciati.
- [ ] In ogni scuola c’è almeno un bocciato in tutte le classi.
- [ ] C’è almeno una scuola che ha almeno un bocciato in ogni classe.
- [ ] C’è almeno una scuola in cui c’è una classe che ha almeno un bocciato. (I Giochi di Archimede, 1999)
- Se il pomeriggio ho giocato a tennis, la sera ho fame e se la sera ho fame,
allora mangio troppo. Quale delle seguenti conclusioni non posso trarre da
queste premesse?
- [ ] Se gioco a tennis il pomeriggio, allora la sera ho fame e mangio troppo
- [ ] se la sera ho fame, allora mangio troppo, oppure ho giocato a tennis il pomeriggio
- [ ] se la sera non ho fame, allora non ho giocato a tennis il pomeriggio
- [ ] se la sera non ho fame, allora non mangio troppo
- [ ] se la sera non mangio troppo, allora non ho giocato a tennis il pomeriggio.(I Giochi di Archimede, 1997)
- Su un isola vivono tre categorie di persone: i cavalieri, che dicono sempre
la verità, i furfanti, che mentono sempre, ed i paggi che dopo una verità
dicono sempre una menzogna e viceversa. Sull’isola incontro un vecchio, un
ragazzo e una ragazza. Il vecchio afferma: “Io sono paggio”; “Il
ragazzo è cavaliere”. Il ragazzo dice: “Io sono cavaliere”; “La
ragazza è paggio”. La ragazza afferma infine: “Io sono furfante”;
“Il vecchio è paggio”. Si può allora affermare che:
- [ ] c’è esattamente un paggio
- [ ] ci sono esattamente due paggi
- [ ] ci sono esattamente tre paggi
- [ ] non c’è alcun paggio
- [ ] il numero dei paggi non è sicuro.(I Giochi di Archimede, 1998)
