Gli enti fondamentali della geometria¶
In questo paragrafo diamo un cenno del sistema assiomatico della geometria razionale facendo riferimento principalmente all’impostazione assiomatica di Hilbert.
Concetti primitivi¶
Sono concetti primitivi per la geometria il punto, la retta e il piano. Di essi non si dà una definizione e costituiscono la base per definire tutti gli altri enti della geometria.
Oltre a questi tre enti primitivi occorre poi assumere l’esistenza di tre relazioni primitive tra gli enti geometrici: giacere su, stare fra, essere congruente a. Queste relazioni permettono di stabilire dei legami tra gli enti geometrici, per esempio: “un punto giace su una retta”, “un punto sta fra altri due punti”, “un segmento è congruente a un altro segmento”, …
Esiste una simbologia convenzionale condivisa dagli studiosi per indicare questi enti:
- per indicare un punto usiamo una lettera maiuscola, A, B, C, …;
- per indicare una retta usiamo una lettera minuscola, a, b, c, …;
- per indicare un piano usiamo una lettera greca:
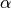 ,
,
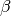 ,
,
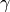 ...
...
Ricordiamo l’alfabeto greco, per gli studenti che hanno poca familiarità con esso:
Lettere greche minuscole:
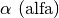 ,
,
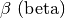 ,
,
 ,
,
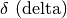 ,
,
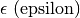 ,
,
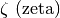 ,
,
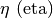 ,
,
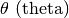 ,
,
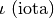 ,
,
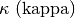 ,
,
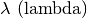 ,
,
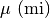 ,
,
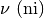 ,
,
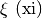 ,
,
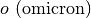 ,
,
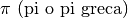 ,
,
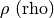 ,
,
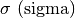 ,
,
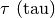 ,
,
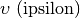 ,
,
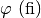 ,
,
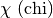 ,
,
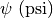 ,
,
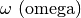 .
.
Lettere greche maiuscole:
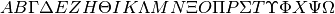 .
.
Per il simbolo di congruenza si usa
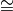
- Degli enti fondamentali Euclide aveva dato le seguenti definizioni:
- Punto è ciò che non ha parti.
- Linea è lunghezza senza larghezza.
- Superficie piana è quella che giace ugualmente rispetto alle rette su di essa.
Le definizioni in questo caso sono utili per farci un’idea intuitiva di essi. Tuttavia, come è già stato detto in precedenza, e da quanto si intuisce osservando le definizioni euclidee, per definire il punto si utilizza la nozione di parte: punto è ciò che non ha parti. Occorrerebbe quindi definire che cosa è una parte. Ma per definire un parte avremmo bisogno di altre nozioni di partenza, in un procedimento senza fine. Per questo motivo nell’impostazione assiomatica moderna si preferisce non dare la definizione dei tre enti primitivi e ‘definirli implicitamente’ attraverso le proprietà di cui godono. Ciò significa che si preferisce dare maggiore importanza a come essi si comportano e cosa possiamo fare con essi, piuttosto che descrivere cosa sono.
Dal punto di vista della rappresentazione grafica si usano le seguenti convenzioni:
Rappresentazione grafica degli enti fondamentali della geometria.
Postulati¶
Un postulato, o assioma, è una proposizione, spesso intuitiva, evidente ma non dimostrata, ammessa come vera in quanto necessaria per costruire poi le dimostrazioni dei teoremi.
Euclide nei suoi Elementi aveva individuato un gruppo di cinque assiomi, che riguardano le nozioni comuni e quindi non fanno riferimento alla geometria, e un gruppo di cinque postulati che riguardano proprietà geometriche.
Assiomi di Euclide¶
- Cose che sono uguali a una stessa cosa sono uguali anche tra loro.
- Se cose uguali sono addizionate a cose uguali, le totalità sono uguali.
- Se da cose uguali sono sottratte cose uguali, i resti sono uguali.
- Cose che coincidono fra loro sono uguali.
- Il tutto è maggiore della parte.
Postulati di Euclide¶
- Si possa condurre una linea retta da un qualsiasi punto ad ogni altro punto.
- Un segmento si possa prolungare indefinitamente in linea retta.
- Si possa descrivere un cerchio con qualsiasi centro e qualsiasi raggio.
- Tutti gli angoli retti siano uguali tra loro.
- Se una retta che taglia due rette forma dallo stesso lato angoli interni la cui somma è minore di due angoli retti, prolungando illimitatamente le due rette, esse si incontreranno dalla parte dove i due angoli sono minori di due retti.
Nell’impostazione assiomatica moderna di Hilbert, gli assiomi hanno la funzione di definire implicitamente gli enti primitivi, cioè di fissare le proprietà alle quali questi enti devono soddisfare. Hilbert aggiunge inoltre altri assiomi che Euclide stesso non aveva esplicitato chiaramente.
Assiomi di Hilbert¶
L’esposizione che segue è una semplificazione degli assiomi del grande matematico tedesco; chi vuole studiare direttamente il testo originale può consultare http://www.gutenberg.org/files/17384/17384-pdf.pdf [ultima consultazione 26.02.2012].
Hilbert assume come enti primitivi della geometria piana il punto e la retta, come relazioni primitive l’appartenenza di un punto ad una retta, il giacere di un punto tra altri due punti, e la congruenza di segmenti.
Assiomi di appartenenza: “giacere su”:
I. Dati due punti distinti, esiste una e una sola retta che contiene entrambi i punti.
II. Ogni retta contiene almeno due punti. Esistono almeno tre punti che non giacciono su questa retta.
Due punti A e B giacciono sempre su un retta, questa retta è unica, esiste sempre almeno un terzo punto C che non giace sulla retta r.
III. Dati tre punti non allineati, esiste uno e un solo piano che contiene tutti e tre i punti. Ogni piano contiene almeno un punto.
Per tre punti non allineati, A, B, C, passa un piano
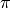 , questo piano è unico.
, questo piano è unico.
IV. Se due punti di una retta giacciono su un piano, allora anche tutti gli altri punti della retta giacciono su questo piano.
Se i punti A e B giacciono sul piano
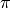 , tutti i punti della retta r, che contiene i punti A e B, giacciono sul piano
, tutti i punti della retta r, che contiene i punti A e B, giacciono sul piano
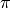 .
.
V. Se un punto giace su due piani distinti, allora esiste almeno un altro punto giacente su entrambi questi piani.
- Esistono almeno quattro punti che non giacciono sullo stesso piano.
Assiomi di ordinamento: “stare fra”:
VII. Se un punto B giace fra i punti A e C, allora i punti A, B e C sono tre punti distinti sulla stessa retta, e B giace fra C ed A.
Se B sta tra A e C, allora sta anche tra C e A, e i tre punti sono allineati.
VIII. Dati due punti A e C, esiste almeno un punto B, sulla retta AC, giacente fra di essi.
XI. Dati tre punti qualsiasi di una retta, uno e uno solo di essi giace fra gli altri due.
Gli ultimi assiomi ci permettono di dedurre il seguente
TEOREMA. Tra due punti di una retta esiste sempre una quantità illimitata di altri punti.
Dimostrazione
Data una retta r e due suoi punti A e B, per l’assioma VIII sappiamo che esiste un terzo punto C sulla retta r che giace tra A e B. Ma allora esiste un punto D su r che giace tra A e C e un punto E che giace tra C e B. Per lo stesso assioma esisterà un punto tra A e D, uno tra D e C, uno tra C e B, e così via.
DEFINIZIONE. Si chiama segmento AB l’insieme dei punti A e B e di tutti quelli che stanno stanno sulla retta tra A e B.
Gli assiomi di ordinamento ci permettono di dare anche la seguente
DEFINIZIONE. Presi quattro punti ABCO su una retta, in modo che B stia tra A e O e O stia tra A e C possiamo dire che A e B**stanno dalla medesima parte rispetto a**O, mentre A e C non stanno dalla medesima parte rispetto a O.
A e B stanno dalla medesima parte rispetto a O; A e C non stanno dalla medesima parte rispetto a O.
Trascuriamo in questa trattazione elementare l’Assioma di Pasch (X) e l’Assioma delle parallele (XI)
Assiomi di congruenza: “essere congruente a”
XII. Assioma del trasporto di un segmento. Se A, B sono due punti di una retta a e A’ è un punto sulla stessa retta (o fissato su un’altra retta a’), si può sempre trovare un punto B’ sulla retta a (o su a’), da una data parte rispetto ad A’, tale che il segmento AB sia congruente al segmento A’B’.
Assioma del trasporto di un segmento.
XIII. La relazione di congruenza tra segmenti è transitiva, cioè se
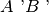 e
e
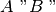 sono congruenti ad AB, allora A’B’è congruente a A’‘B’‘.
sono congruenti ad AB, allora A’B’è congruente a A’‘B’‘.
XIV. Siano
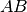 e
e
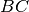 segmenti su una retta
segmenti su una retta
 privi di punti comuni a parte B, e siano A’B’ e B’C’ segmenti su una retta
privi di punti comuni a parte B, e siano A’B’ e B’C’ segmenti su una retta
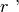 privi di punti comuni a parte
privi di punti comuni a parte
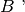 . Se e
. Se e
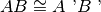
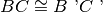 , allora
, allora
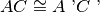 .
.
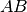 e
e
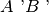 sono segmenti congruenti, anche
sono segmenti congruenti, anche
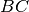 e
e
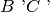 sono segmenti congruenti, allora
sono segmenti congruenti, allora
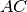 e
e
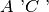 sono segmenti congruenti.
sono segmenti congruenti.
Prima di proseguire con gli altri assiomi premettiamo la seguente
DEFINIZIONE. Chiamiamo semiretta la parte di retta costituita da un punto di essa, detto origine della semiretta, e da tutti i punti che stanno dalla stessa parte rispetto all’origine.
DEFINIZIONE. Si dice angolo ciascuna delle due parti in cui un piano è diviso da due semirette aventi l’origine in comune; le semirette si dicono lati dell’angolo; l’origine comune alle due semirette si dice vertice dell’angolo.
Le semirette r e s, aventi l’origine V comune individuano due regioni del piano dette angolo.
L’angolo individuato da tre punti
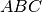 è l’angolo formato dalla semiretta con origine
è l’angolo formato dalla semiretta con origine
 e passante per
e passante per
 e dalla semiretta con origine
e dalla semiretta con origine
 e passante per
e passante per
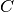 . Questo angolo si indica con il simbolo .
. Questo angolo si indica con il simbolo .
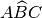 Graficamente si usa indicare un angolo con un archetto.
Graficamente si usa indicare un angolo con un archetto.
XV. Dati un angolo
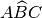 ed una semiretta B’C’ , esistono e sono uniche due semirette B’D e B’E, tali che
l’angolo
ed una semiretta B’C’ , esistono e sono uniche due semirette B’D e B’E, tali che
l’angolo
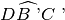 è congruente all’angolo
è congruente all’angolo
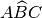 e l’angolo
e l’angolo
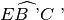 è congruente all’angolo
è congruente all’angolo
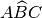 .
.
XV, dato
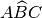 è possibile costruire gli angoli
è possibile costruire gli angoli
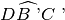 e
e
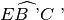 congruenti ad
congruenti ad
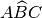 ed aventi un lato su una semiretta prefissata.
ed aventi un lato su una semiretta prefissata.
XVI. La relazione di congruenza tra angoli è transitiva, cioè se
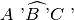 e
e
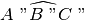 sono congruenti ad
sono congruenti ad
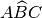 , allora
, allora
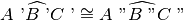 .
.
Assiomi di continuità
- Assioma di Archimede. Sulla retta che unisce due punti qualsiasi A e B si
prende un punto A1, si prendono poi i punti A2, A3, A4, … in modo che A1
sta tra A e A2, A2 sta tra A1 e A3, A3 tra A2 e A4 ecc. e che
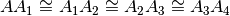 ecc. Allora tra tutti questi punti esiste sempre un certo punto An tale che B
sta tra A e An.
ecc. Allora tra tutti questi punti esiste sempre un certo punto An tale che B
sta tra A e An.
Figura 16. Dati i punti A e B sulla retta r si può sempre costruire la
serie di segmenti
congruenti
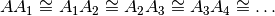 in modo da superare il punto B.
in modo da superare il punto B.
Assioma di completezza
- Ad un sistema di punti, linee rette e piani è impossibile aggiungere altri elementi in modo tale che il sistema, così generalizzato, formi una nuova geometria obbediente a tutti i cinque gruppi di assiomi. In altre parole gli elementi della geometria formano un sistema che non è suscettibile di estensione, nel caso in cui si considerino validi i cinque gruppi di assiomi.
Esercizi¶
- Su un isola vivono tre categorie di persone: i cavalieri, che dicono sempre
la verità, i furfanti, che mentono sempre, ed i paggi che dopo una verità
dicono sempre una menzogna e viceversa. Sull’isola incontro un vecchio, un
ragazzo e una ragazza. Il vecchio afferma: “Io sono paggio”; “Il
ragazzo è cavaliere”. Il ragazzo dice: “Io sono cavaliere”; “La
ragazza è paggio”. La ragazza afferma infine: “Io sono furfante”;
“Il vecchio è paggio”. Si può allora affermare che:
- [ ] c’è esattamente un paggio
- [ ] ci sono esattamente due paggi
- [ ] ci sono esattamente tre paggi
- [ ] non c’è alcun paggio
- Gli enti primitivi della geometria sono quelli
- [ ] Che occorre definire
- [ ] Che occorre dimostrare
- [ ] Che non si definiscono
- [ ] Che si conoscono già per averli studiati prima
- Gli assiomi sono
- [ ] Proposizioni note che si preferisce non dimostrare per non appesantire lo studio
- [ ] Proposizioni che è necessario dimostrare
- [ ] Proposizioni che si assumono vere senza dimostrazione
- [ ] Proposizioni che non si definiscono
- [ ] Proposizioni che non si dimostrano perché la loro dimostrazione è molto semplice
- Quali delle seguenti affermazioni sono vere?
- Due punti sono sempre allineati.. tabVF
- Tre punti sono sempre allineati.. tabVF
- Tre punti sono sempre complanari.. tabVF
- Tre punti allineati individuano un unico piano.. tabVF
- Una retta e un punto esterno ad essa individuano un piano.. tabVF
- Distingui nelle seguenti frasi le definizioni dalle proposizioni o proprietà
- La Terra ruota su se stessa in un giorno... tabDP
- Il solstizio è il momento in cui il Sole raggiunge, nel suo moto apparente lungo l’eclittica, il punto dideclinazione massima o minima... tabDP
- La cellula è l’unità fondamentale di tutti gli organismi viventi... tabDP
- I virus sono responsabili di alcune malattie... tabDP
- I numeri che hanno per ultima cifra 0 sono numeri pari... tabDP
- Un numero si dice pari se è divisibile per 2... tabDP
- Su una retta si segnano quattro punti ABCD, quanti segmenti restano individuati?
- Date tre semirette a, b, c aventi la stessa origine O, quanti angoli restano individuati?
- Unisci in tutti i modi possibili mediante rette tre punti non allineati e posti sullo stesso piano.
- Unisci in tutti i modi possibili mediante rette quattro punti, a tre a tre non allineati, di uno stesso piano.
- Quattro rette a due a due incidenti quanti punti di intersezioni individuano complessivamente?
- Quale assioma è rappresentato in figura?
- [ ] tre punti distinti non allineati determinano uno ed un solo piano che li contiene
- [ ] su un piano esistono infiniti punti ed infinite rette
- [ ] la retta passante per due punti distinti di un piano giace completamente nel piano
- [ ] su una retta esistono infiniti punti
- Rispondi a voce alle seguenti domande
- Qual è l’origine della parola geometria?
- Qual è la differenza tra assioma e teorema?
- Qual è la differenza tra ente definito e ente primitivo?