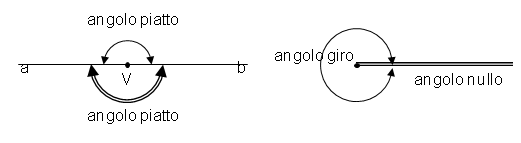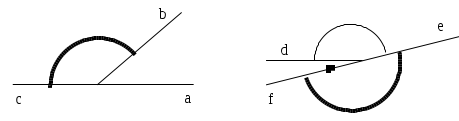Prime definizioni: segmenti e angoli¶
Semirette e segmenti¶
Nel paragrafo precedente abbiamo già introdotto alcune definizioni di base, necessarie per enunciare tutti i postulati della geometria secondo l’assiomatizzazione di Hilbert. In questo paragrafo costruiamo le prime definizioni. Per comodità del lettore riportiamo anche quelle già date.
Partiamo dalla nozione generica di figura.
DEFINIZIONE. Si chiama figura un qualsiasi insieme, non vuoto, di punti.
Questa definizione fa riferimento soltanto all’ente primitivo geometrico di punto.
Lo spazio non è considerato un ente primitivo, in quanto può essere ottenuto dalla seguente definizione.
DEFINIZIONE. Si chiama spazio l’insieme di tutti i punti.
Risulta pertanto che una figura è un qualsiasi sottoinsieme dello spazio.
In base agli assiomi di ordinamento un qualunque punto P su una retta divide la retta in due parti, una è costituita dai punti che ‘seguono’ P, l’altra è costituita dai punti che ‘precedono’ P.
DEFINIZIONE. Si chiama semiretta la parte di retta costituita da un punto di essa, detto origine della semiretta, e da tutti i punti che stanno dalla stessa parte rispetto all’origine.
Solitamente, la semiretta si indica con una lettera latina minuscola.
Prendendo due qualsiasi rette dello spazio esse si possono trovare in diverse posizioni reciproche, cioè una rispetto all’altra.
DEFINIZIONE. Due rette si dicono complanari se appartengono a uno stesso piano; se non appartengono a uno stesso piano si dicono sghembe.
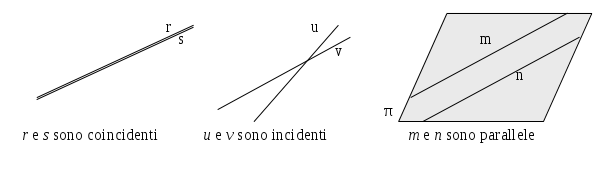
Due rette complanari si dicono incidenti se hanno uno, e uno solo, punto in comune.
Due rette complanari che non hanno nessun punto in comune si dicono parallele.
Se due rette hanno almeno due punti in comune sono coincidenti.
Per indicare che le rette r e s sono parallele si usa il simbolo r//s.
Fai attenzione al fatto che due rette non parallele possono appartenere a piani diversi, in questo caso non avranno punti in comune, sono cioè sghembe. Viceversa se due rette hanno un punto in comune allora sono sicuramente complanari. Inoltre, se hanno più di un punto in comune le rette coincidono, in questo caso ci sono infiniti piani che le contengono.
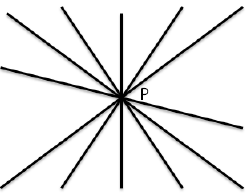
DEFINIZIONE. L’insieme di tutte le rette di un piano che passano per uno stesso punto è detto fascio proprio di rette, il punto in comune a tutte le rette si dice centro del fascio.
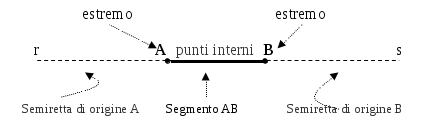
Prendendo due punti su una retta, A e B, la retta resta divisa in tre parti: la semiretta di origine A che non contiene B, la parte costituita dai punti compresi tra A e B e la semiretta di origine B che non contiene A.
DEFINIZIONE. Si chiama segmento AB l’insieme dei punti A e B e di tutti quelli che stanno tra A e B.I punti A e B si dicono estremi del segmento.
I punti A e B formano le due semirette,* r* e* s*, e il segmento AB.
Un segmento viene indicato con le due lettere maiuscole dei suoi estremi.
Due segmenti nel piano possono trovarsi in diverse posizioni reciproche. Alcune di esse hanno un interesse per la geometria.
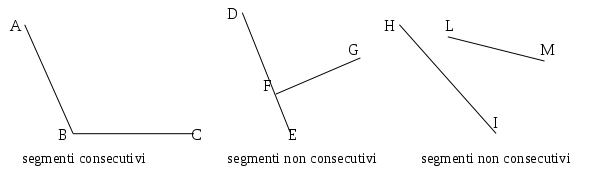
DEFINIZIONE. Due segmenti si dicono consecutivi se hanno in comune soltanto un estremo.
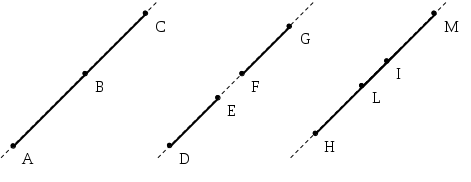
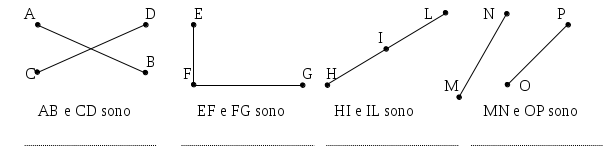
I segmenti AB e BC sono consecutivi perché hanno in comune solo il punto B che è un estremo di entrambi; DE e FG non sono consecutivi perché hanno in comune solo il punto F ma esso non è estremo del segmento DE; HI e LM non sono consecutivi perché non hanno nessun punto in comune.
DEFINIZIONE. Due segmenti si dicono adiacenti se sono consecutivi ed appartengono alla stessa retta.
I segmenti AB e BC sono adiacenti perché hanno in comune solo l’estremo B e giacciono sulla stessa retta; i segmenti DE e FG non sono adiacenti; i segmenti HI e LM non sono adiacenti.
Semipiani e angoli¶
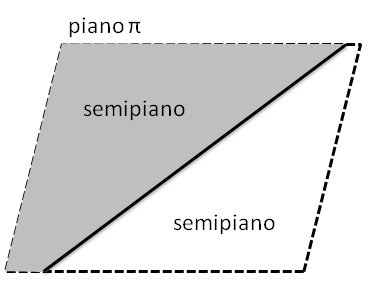
DEFINIZIONE. Si dice semipiano di origine la retta r la figura formata dalla retta r e da una delle due parti in cui essa divide il piano.
In un piano
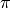 , una qualsiasi retta
, una qualsiasi retta
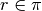 dà origine a due semipiani distinti, che si dicono semipiani opposti.
dà origine a due semipiani distinti, che si dicono semipiani opposti.
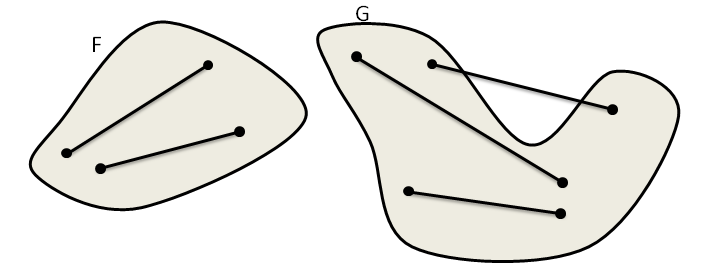
DEFINIZIONE. Una figura si dice convessa se, considerati due suoi qualsiasi punti, il segmento che li unisce è contenuto nella figura. Si dice concava se esistono almeno due punti per i quali il segmento che li unisce non è interamente contenuto nella figura.
La figura F è convessa, per qualsiasi coppia di punti interni a F il segmento che li unisce è interamente nella figura; la figura G è concava perché unendo i punti P e Q si ha un segmento che cade in parte esternamente alla figura.
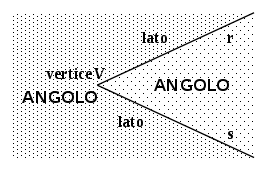
DEFINIZIONE. Si dice angolo ciascuna delle due parti in cui un piano è diviso da due semirette aventi l’origine in comune; le semirette si dicono lati dell’angolo; l’origine comune alle due semirette si dice vertice dell’angolo.
Le semirette r e s, aventi l’origine V comune individuano due regioni del piano dette angolo.
DEFINIZIONEUn angolo si dice angolo piatto se i suoi lati sono uno il prolungamento dell’altro.
Un angolo si dice angolo nullo se è costituito solo da due semirette sovrapposte.
Si dice angolo giro l’angolo che ha per lati due semirette sovrapposte e che contiene tutti i punti del piano.
L’angolo
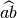 a sinistra è piatto, gli angoli a destra sono rispettivamente un angolo giro e
un angolo nullo.
a sinistra è piatto, gli angoli a destra sono rispettivamente un angolo giro e
un angolo nullo.
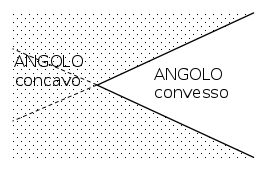
DEFINIZIONE. Un angolo, i cui lati non appartengono alla stessa retta, si dice concavo se contiene i prolungamenti dei lati, se non li contiene si dice convesso.
L’angolo concavo è quello punteggiato in quanto contiene i prolungamenti dei lati.
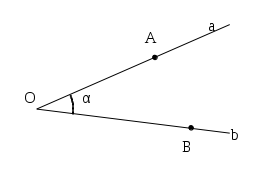
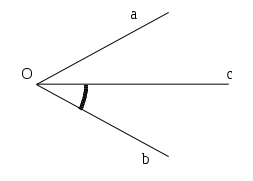
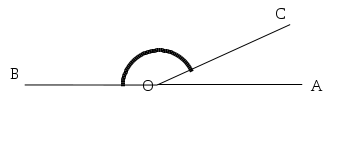
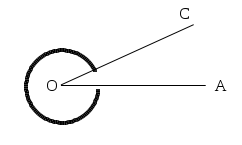
Quando si disegna un angolo è utile, oltre a disegnare le semirette e l’origine, indicare con un archetto quale dei due angoli si intende considerare.
Per indicare che l’angolo da considerare è quello convesso e non quello concavo si è usato un archetto in prossimità del vertice O.
Per indicare gli angoli si usano diverse convenzioni:
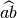 se si conoscono i nomi delle semirette che ne costituiscono i lati;
se si conoscono i nomi delle semirette che ne costituiscono i lati;
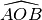 se si conoscono i nomi del vertice e di due punti sui lati;
se si conoscono i nomi del vertice e di due punti sui lati;
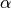
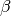
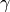 , ... una lettera greca per indicare direttamente l’angolo.
, ... una lettera greca per indicare direttamente l’angolo.
I primi due modi di indicare l’angolo non individuano con chiarezza di quale dei due angoli si tratta. Solitamente si intende l’angolo convesso, quando si vuole indicare l’angolo concavo bisogna dirlo esplicitamente.
Anche per gli angoli si danno le definizioni di angoli consecutivi e angoli adiacenti, in parte simili a quelle date per i segmenti.
DEFINIZIONE. Due angoli si dicono angoliconsecutivi se hanno il vertice e un lato comune e giacciono da parte opposta rispetto al lato comune.
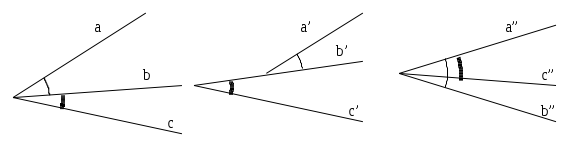
Nella figura gli angoli
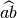 e
e
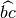 sono consecutivi perché hanno il vertice e il lato b in comune;
sono consecutivi perché hanno il vertice e il lato b in comune;
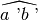 e
e
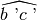 non sono consecutivi perché non hanno il vertice in comune;
non sono consecutivi perché non hanno il vertice in comune;
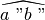 e
e
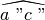 non sono consecutivi perché non giacciono da parti opposte rispetto al lato in
comune
non sono consecutivi perché non giacciono da parti opposte rispetto al lato in
comune
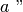 .
.
DEFINIZIONE. Due angoli si dicono angoliadiacenti se sono consecutivi e se i lati non comuni giacciono sulla stessa retta.
I due angoli
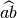 e
e
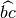 sono adiacenti, perché sono consecutivi e i lati
sono adiacenti, perché sono consecutivi e i lati
 e
e
 sono uno il prolungamento dell’altro; i due angoli
sono uno il prolungamento dell’altro; i due angoli
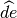 ed
ed
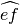 non sono adiacenti in quanto
non sono adiacenti in quanto
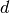 non è il prolungamento di
non è il prolungamento di
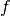 ; gli angoli
; gli angoli
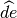 e
e
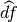 sono adiacenti in quanto
sono adiacenti in quanto
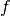 è il prolungamento di
è il prolungamento di
 .
.
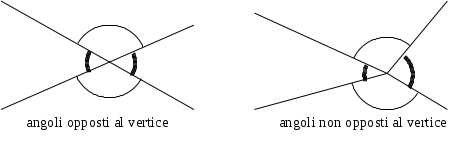
DEFINIZIONE. Due angoli convessi si dicono angoli opposti al vertice se i lati del primo sono i prolungamenti dei lati dell’altro.
Gli angoli formati dalle semirette a sinistra sono opposti al vertice; gli angoli formati dalle semirette a destra non lo sono.
Posizioni reciproche di semipiani¶
Siano
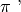 e
e
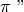 due semipiani di un piano
due semipiani di un piano
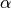 , aventi per origine rispettivamente le rette
, aventi per origine rispettivamente le rette
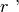 e
e
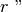 . La loro unione e la loro intersezione danno luogo a figure diverse tra loro a
seconda dei vari casi possibili.
. La loro unione e la loro intersezione danno luogo a figure diverse tra loro a
seconda dei vari casi possibili.
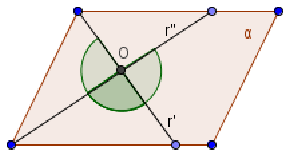
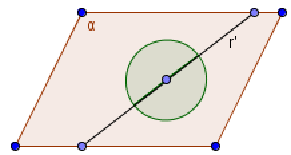
1° caso
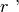 e
e
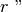 sono incidenti in un punto
sono incidenti in un punto
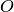 . Allora l’intersezione dei due semipiani
. Allora l’intersezione dei due semipiani
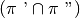 è un angolo convesso di vertice
è un angolo convesso di vertice
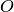 , mentre la loro unione
, mentre la loro unione
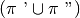 è un angolo concavo di vertice
è un angolo concavo di vertice
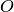 .
.
Le due semirette
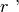 e
e
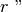 , origini dei semipiani
, origini dei semipiani
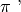 e
e
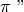 sono incidenti; in questo caso l’unione dei due semipiani è l’angolo
concavo di colore grigio chiaro, la loro intersezione è l’angolo convesso di
colore grigio scuro.
sono incidenti; in questo caso l’unione dei due semipiani è l’angolo
concavo di colore grigio chiaro, la loro intersezione è l’angolo convesso di
colore grigio scuro.
2° caso
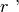 e
e
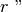 sono coincidenti,
sono coincidenti,
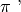 e
e
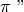 anch’essi coincidenti, cioè perfettamente sovrapposti. In questo caso
particolare l’intersezione e l’unione dei due semipiani coincidono con gli
semipiani
anch’essi coincidenti, cioè perfettamente sovrapposti. In questo caso
particolare l’intersezione e l’unione dei due semipiani coincidono con gli
semipiani
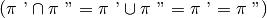 .
.
Osserva che un semipiano è anche un angolo piatto.
I due semipiani hanno la stessa retta di origine e sono anche coincidenti: la loro unione e la loro intersezione coincide con i semipiani stessi e formano lo stesso angolo piatto.
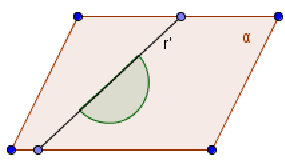
3° caso
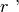 e
e
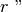 sono coincidenti, con
sono coincidenti, con
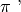 e
e
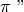 distinti, e dunque opposti. In tal caso particolare l’intersezione dei due
semipiani coincide con la retta origine in comune
distinti, e dunque opposti. In tal caso particolare l’intersezione dei due
semipiani coincide con la retta origine in comune
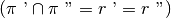 e l’unione di essi coincide con l’intero piano
e l’unione di essi coincide con l’intero piano
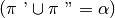 . Notiamo che un piano è anche un angolo giro.
. Notiamo che un piano è anche un angolo giro.
Figura 33. I due semipiani hanno la stessa retta di origine e si trovano da parti opposte: la loro unione coincide con l’intero piano (angolo giro).
4° caso
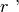 e
e
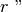 sono parallele e distinte, cioè non hanno punti in comune, ed inoltre
sono parallele e distinte, cioè non hanno punti in comune, ed inoltre
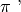 non contiene
non contiene
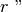 e
e
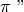 non contiene
non contiene
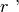 . In tal caso i due semipiani non hanno punti in comune, cioè la loro
intersezione è vuota
. In tal caso i due semipiani non hanno punti in comune, cioè la loro
intersezione è vuota
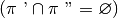 mentre la loro unione è una parte “sconnessa” del piano
mentre la loro unione è una parte “sconnessa” del piano
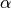 costituita da tutti i punti di
costituita da tutti i punti di
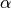 tranne la parte convessa delimitata dalle due semirette
tranne la parte convessa delimitata dalle due semirette
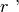 e
e
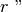 .
.
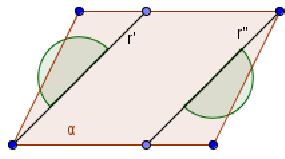
Figura 34. Le rette di origine sono parallele e distinte, i semipiani non hanno punti in comune, la loro unione è costituita dall’unione dei due angoli piatti indicati con un archetto grigio.
5° caso
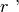 e
e
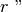 sono parallele e distinte, cioè non hanno punti in comune, ed inoltre
sono parallele e distinte, cioè non hanno punti in comune, ed inoltre
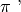 contiene
contiene
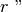 e
e
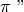 non contiene
non contiene
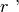 (o viceversa). In tal caso l’intersezione dei due semipiani coincide con uno
dei due semipiani e la loro unione coincide con l’altro semipiano
(o viceversa). In tal caso l’intersezione dei due semipiani coincide con uno
dei due semipiani e la loro unione coincide con l’altro semipiano
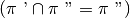 e
e
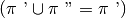 o
o
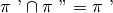 e
e
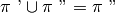 .
.
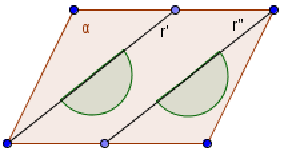
Figura 35. Le rette di origine sono parallele e distinte, uno dei due
semipiani contiene
l’altro; la loro unione è l’angolo piatto con lati sulla retta
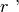 , la loro intersezione è l’angolo piatto con lati sulla retta
, la loro intersezione è l’angolo piatto con lati sulla retta
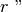
6° caso
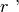 e
e
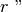 sono parallele e distinte, cioè non hanno punti in comune, ed inoltre
sono parallele e distinte, cioè non hanno punti in comune, ed inoltre
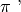 contiene
contiene
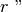 e
e
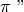 contiene
contiene
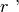 . In tal caso l’unione dei due semipiani è l’intero piano
. In tal caso l’unione dei due semipiani è l’intero piano
 , mentre l’intersezione di essi è la parte (convessa) di
, mentre l’intersezione di essi è la parte (convessa) di
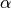 delimitata dalle due semirette
delimitata dalle due semirette
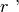 e
e
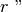 . Tale intersezione
. Tale intersezione
 prende il nome di striscia di piano delimitata dalle rette
prende il nome di striscia di piano delimitata dalle rette
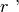 e
e
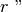 che sono dette lati della striscia.
che sono dette lati della striscia.
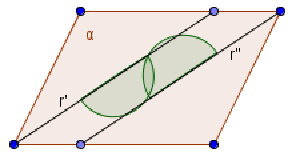
Figura 36. Le rette di origine sono parallele e distinte, ognuno dei due
semipiani
contiene l’altra retta, la loro unione è formata da tutto il piano, la loro
intersezione forma una striscia di piano, delimitata dalle rette
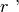 e
e
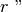 , dette lati della striscia.
, dette lati della striscia.
Confronto e operazioni fra segmenti e angoli¶
Premessa intuitiva¶
Nel linguaggio comune usiamo la parola ‘uguale’ con un significato generico,
spesso per indicare due oggetti che si assomigliano: due macchine uguali, due
orologi uguali, … In aritmetica e in algebra usiamo la parola ‘uguale’ per
indicare oggetti matematici perfettamente uguali. Per esempio,
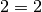 , ogni numero infatti è uguale solo a se stesso. Scriviamo anche
, ogni numero infatti è uguale solo a se stesso. Scriviamo anche
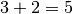 , per dire che il numero che si ottiene dalla somma di
, per dire che il numero che si ottiene dalla somma di
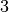 e
e
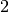 è proprio il numero
è proprio il numero
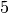 . Nei polinomi si enuncia il principio di identità dei polinomi, in base al
quale due polinomi sono uguali se si possono scrivere formalmente allo stesso
modo.
. Nei polinomi si enuncia il principio di identità dei polinomi, in base al
quale due polinomi sono uguali se si possono scrivere formalmente allo stesso
modo.
In geometria, usiamo il termine ‘uguale’ per indicare due figure coincidenti nella forma e nella posizione. In altre parole due figure sono uguali solo se sono esattamente la stessa figura. Tuttavia, in geometria siamo interessati a studiare soprattutto figure che senza essere del tutto identiche hanno delle caratteristiche in comune. Vediamo prima degli esempi intuitivi e successivamente tratteremo lo stesso tema ma in modo formalmente corretto.
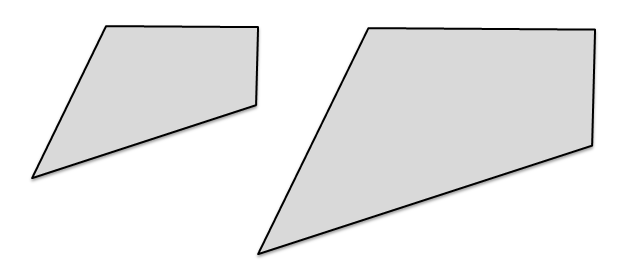
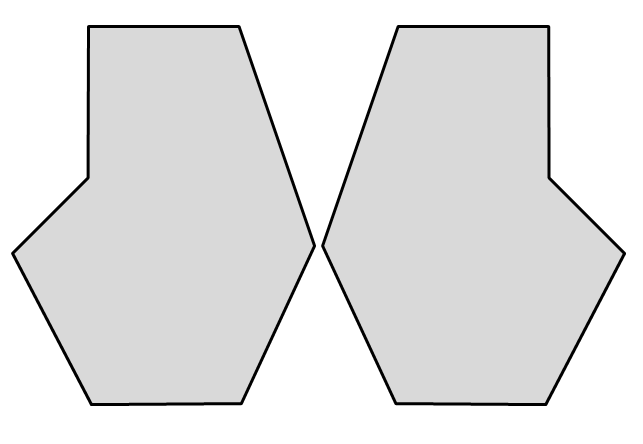
Le figure a lato hanno la stessa forma ma una è più grande dell’altra, la seconda infatti è stata ottenuta dalla prima raddoppiando i lati: in geometria si dicono simili.
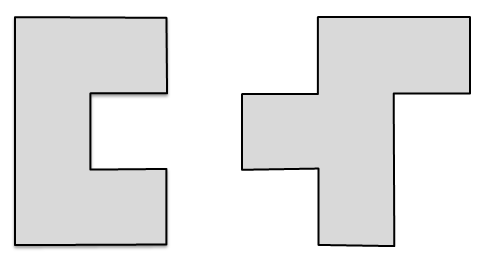
Queste due altre figure non hanno la stessa forma, non si somigliano affatto, però le loro superfici hanno la stessa estensione, in quanto sono costituite dallo stesso numero di quadratini: in geometria si dicono equivalenti.
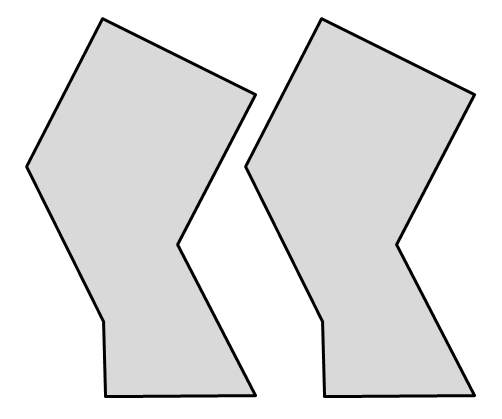
Le figure a lato hanno la stessa forma e le stesse dimensioni ma sono in posizioni differenti, è però possibile spostare una sull’altra senza deformarle e farle coincidere. Usualmente le chiamiamo figure uguali, in geometria si dicono congruenti.
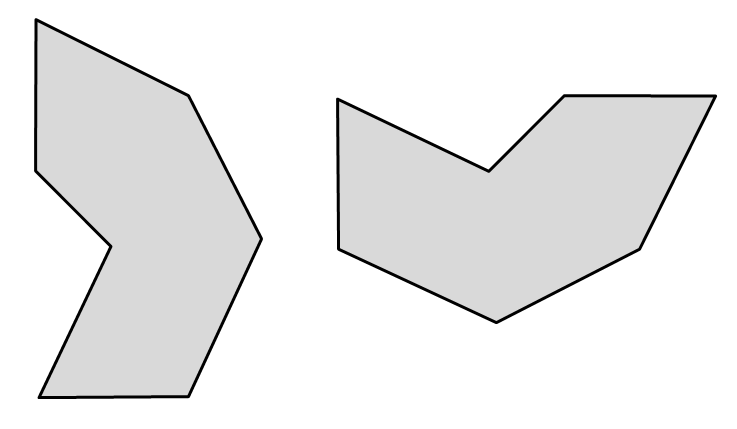
Le due figure a lato hanno la stessa forma e le stesse dimensioni, per rendersene conto occorre ruotare per esempio la seconda figura in senso antiorario (si può ruotare anche in senso orario ma di un angolo maggiore) e poi trascinarla sulla prima per sovrapporla. Anche queste figure sono dette uguali nel linguaggio comune, in geometria si dicono congruenti.
Le due figure a lato hanno stessa forma e stesse dimensioni, tuttavia non si riesce a trasportare l’una sull’altra muovendole nel piano, né trascinandole, né ruotandole, occorre ribaltarne una facendola uscire dal piano; le due figure sono una l’immagine speculare dell’altra. In geometria, se due figure piane sono tali che, spostandone una senza deformarla, possono essere poste in maniera tale che una sia l’immagine speculare dell’altra, diciamo che sono inversamente congruenti.
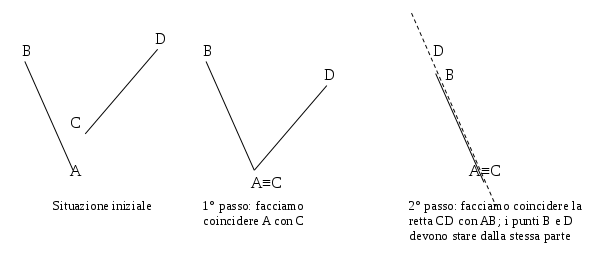
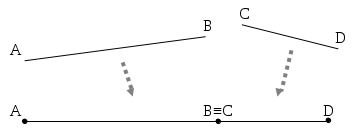
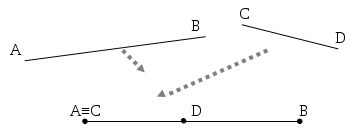
Osserviamo i due segmenti AB e CD rappresentati nella figura che segue. I due segmenti sono sovrapponibili, e quindi congruenti, infatti basta fare scorrere il segmento CD lungo la retta fino a far coincidere C con A, il punto D coinciderà con B. Tuttavia, se portiamo D a coincidere con A dobbiamo poi ribaltare il segmento CD in modo che A coincida con D e B coincida con C.
Figura 42. I segmenti AB e CD sono direttamente congruenti in quanto si può far coincidere A con C e B con D semplicemente facendo scorrere lungo la retta un segmento sull’altro. Se invece vogliamo far coincidere A con D e B con C occorre ribaltare, uscendo fuori dalla retta, uno dei due segmenti.
Osserva che per ribaltare una figura occorre una dimensione in più, precisamente se si tratta di due figure piane occorre avere la terza dimensione per ribaltare una figura piana, se siamo su una retta occorre la seconda dimensione per ribaltare un segmento.
Per renderci conto di quanto accade con le figure solide, possiamo pensare ai palmi delle nostre mani che con buona approssimazione si possono considerare inversamente congruenti: esse possono essere giunte, ma non sovrapposte nel senso in cui si parla a proposito delle figure piane. Infatti non è possibile vedere le proprie mani, entrambe dal dorso o entrambe dal palmo, con le dita rivolte verso l’alto, in modo che in ciascuna di esse il pollice sia a sinistra oppure a destra.
La congruenza¶
Secondo il punto di vista del matematico tedesco Felix Klein (1848-1925), la geometria è lo studio delle proprietà delle figure che sono invarianti rispetto a certe trasformazioni. Nello studio della geometria euclidea, quella che tratteremo in questo Tema, ci occupiamo delle proprietà delle figure geometriche invarianti rispetto ai movimenti rigidi, cioè rispetto a quei movimenti che conservano forma e dimensioni delle figure. Queste trasformazioni vengono anche dette isometrie (si intuisce dalla radice etimologica che si parla di stessa misura): significa che viene stabilita una corrispondenza biunivoca tra i punti di due figure congruenti in modo da “mantenere” le distanze.
DEFINIZIONE. Diciamo che due figure
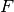 e
e
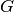 sono congruenti quando esiste un movimento rigido che le sovrappone
perfettamente. In simboli
sono congruenti quando esiste un movimento rigido che le sovrappone
perfettamente. In simboli
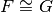 .
.
Nella Premessa a questo paragrafo abbiamo dato un’idea intuitiva e sperimentale del concetto di congruenza. Ma per esplicitarlo matematicamente dobbiamo utilizzare gli assiomi di congruenza di Hilbert che abbiamo enunciato nel Capitolo 1 Paragrafo 2. Ne riportiamo alcuni per comodità del lettore.
Assiomi di congruenza¶
- Assioma del trasporto di un segmento. Se
 ,
,
 sono due punti di una retta a e
sono due punti di una retta a e
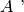 è un punto sulla stessa retta o su un’altra retta
è un punto sulla stessa retta o su un’altra retta
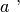 , si può sempre trovare un punto
, si può sempre trovare un punto
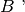 sulla retta a o su
sulla retta a o su
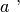 , da una data parte rispetto ad
, da una data parte rispetto ad
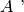 , tale che il segmento
, tale che il segmento
 sia congruente al segmento
sia congruente al segmento
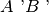 .
.
Questo assioma afferma che, fissato un punto
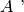 su una retta
su una retta
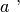 , è sempre possibile trasportare un qualunque segmento
, è sempre possibile trasportare un qualunque segmento
 in modo che l’estremo
in modo che l’estremo
 coincida con
coincida con
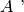 e il segmento stia sulla retta
e il segmento stia sulla retta
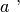 .
.
- La relazione di congruenza tra segmenti è transitiva, cioè se
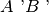 e
e
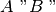 sono congruenti ad
sono congruenti ad
 , allora
, allora
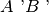 è congruente a
è congruente a
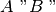 .
.
La relazione di congruenza tra segmenti è allora un relazione di equivalenza, in quanto gode delle proprietà:
- riflessiva: ogni segmento è congruente a se stesso;
simmetrica: se
è congruente a
allora anche
è congruente ad
;
transitiva: se
è congruente ad e
è
congruente ad ,
allora
è congruente ad
.
DEFINIZIONE. Si dice lunghezza di un segmento la classe di equivalenza dei segmenti congruenti tra di loro, cioè l’insieme di tutti i segmenti che sono congruenti tra di loro.
- Assioma del trasporto di un angolo. Dati un angolo
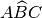 ed una semiretta
ed una semiretta
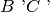 , esistono e sono uniche due semirette
, esistono e sono uniche due semirette
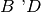 e
e
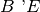 , tali che l’angolo
, tali che l’angolo
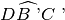 è congruente all’angolo
è congruente all’angolo
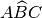 e l’angolo
e l’angolo
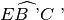 è congruente all’angolo
è congruente all’angolo
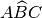 .
.
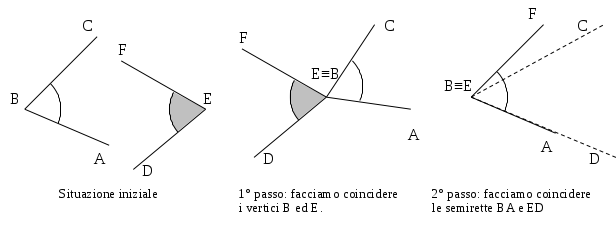
Questo assioma ci garantisce che è sempre possibile trasportare un angolo
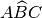 su una qualsiasi semiretta s, facendo coincidere il vertice dell’angolo con
l’origine della semiretta e
un lato dell’angolo con la semiretta s.
su una qualsiasi semiretta s, facendo coincidere il vertice dell’angolo con
l’origine della semiretta e
un lato dell’angolo con la semiretta s.
- La relazione di congruenza tra angoli è transitiva, cioè se
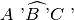 e
e
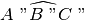 sono congruenti ad
sono congruenti ad
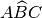 , allora
, allora
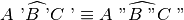 .
.
Quindi anche la relazione di congruenza tra gli angoli è una relazione di equivalenza, gode cioè delle proprietà riflessiva, simmetrica, transitiva.
DEFINIZIONE. Si dice ampiezza di un angolo la classe di equivalenza degli angoli congruenti tra di loro, cioè l’insieme di tutti gli angoli che sono congruenti tra di loro.
Aggiungiamo che:
- Tutte le rette sono fra loro congruenti;
- Tutte le semirette sono fra loro congruenti;
- Tutti i piani sono fra loro congruenti;
Confronto di segmenti¶
Per confrontare l’altezza di due persone e vedere chi è più alto, facciamo mettere affiancate le due persone in modo che i piedi stiano allo stesso livello, dopo di che confrontiamo l’estremità della testa: è più alto chi ha l’estremità della testa più in alto. Un procedimento analogo si fa per confrontare due segmenti.
Per confrontare due segmenti
 e
e
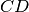 , facciamo in modo che con un movimento rigido gli estremi
, facciamo in modo che con un movimento rigido gli estremi
 e
e
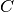 coincidano, con una rotazione intorno al punto A facciamo in modo che coincidano
anche le rette
coincidano, con una rotazione intorno al punto A facciamo in modo che coincidano
anche le rette
 e
e
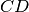 e che gli estremi
e che gli estremi
 e
e
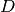 stiano dalla stessa parte rispetto ad
stiano dalla stessa parte rispetto ad
 e
e
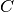 .
.
Confronto di due segmenti
A questo punto possono verificarsi tre situazioni possibili:
 cade dopo l’estremo
cade dopo l’estremo
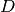 , allora diciamo che
, allora diciamo che
 è maggiore di
è maggiore di
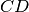 , scriviamo
, scriviamo
 ;
;
 cade esattamente su
cade esattamente su
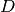 , allora i due segmenti sono congruenti;
, allora i due segmenti sono congruenti;
 cade tra
cade tra
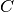 e
e
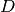 , allora diciamo che
, allora diciamo che
 è minore di
è minore di
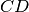 , scriviamo
, scriviamo
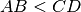 .
.
Confronto di angoli¶
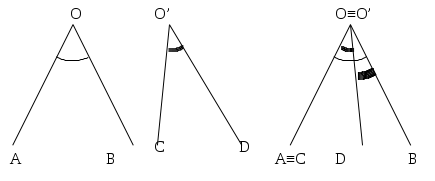
Per confrontare due angoli
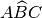 e
e
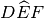 , portiamo con un movimento rigido il vertice
, portiamo con un movimento rigido il vertice
 sul vertice
sul vertice
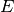 , con una rotazione portiamo a coincidere la semiretta
, con una rotazione portiamo a coincidere la semiretta
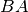 con la semiretta
con la semiretta
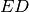 , in modo che le altre due semirette,
, in modo che le altre due semirette,
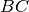 e
e
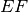 , stiano dalla stessa parte rispetto a
, stiano dalla stessa parte rispetto a
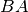 .
.
Confronti di due angoli
A questo punto si possono avere tre situazioni distinte:
- Il lato
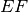 cade internamente all’angolo
cade internamente all’angolo
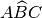 , diciamo che
, diciamo che
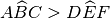 ;
;
Il lato
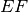 cade esattamente su
cade esattamente su
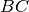 , i due angoli sono congruenti;
, i due angoli sono congruenti;
- Il lato
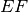 cade esternamente all’angolo
cade esternamente all’angolo
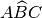 , diciamo che
, diciamo che
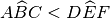 .
.
Operazioni con i segmenti¶
Somma di due segmenti. La somma di due segmenti
 e
e
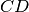 è il segmento
è il segmento
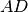 che si ottiene trasportando con un movimento rigido il segmento
che si ottiene trasportando con un movimento rigido il segmento
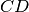 in modo che
in modo che
 e
e
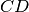 siano adiacenti, con l’estremo
siano adiacenti, con l’estremo
 coincidente con
coincidente con
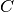 . Scriviamo
. Scriviamo
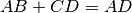 , usando l’usuale simbolo di addizione.
, usando l’usuale simbolo di addizione.
Il segmento
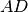 è la somma dei segmenti
è la somma dei segmenti
 e
e
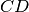 .
.
Differenza di due segmenti. La differenza di due segmenti
 e
e
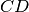 , con
, con
 , è il segmento
, è il segmento
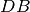 che si ottiene sovrapponendo
che si ottiene sovrapponendo
 e
e
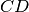 facendo coincidere l’estremo
facendo coincidere l’estremo
 con l’estremo
con l’estremo
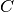 . Scriviamo
. Scriviamo
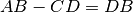
Il segmento
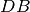 è la differenza tra i segmenti
è la differenza tra i segmenti
 e
e
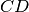 .
.
Multiplo di un segmento. Il multiplo secondo
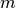 , numero naturale diverso da zero, di un segmento
, numero naturale diverso da zero, di un segmento
 è il segmento
è il segmento
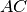 che si ottiene sommando
che si ottiene sommando
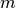 volte il segmento
volte il segmento
 a se stesso.
a se stesso.
In figura
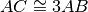
Se
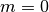 , il multiplo secondo m di qualsiasi segmento
, il multiplo secondo m di qualsiasi segmento
 è il segmento nullo, ove per segmento nullo intendiamo un qualsiasi segmento in
cui gli estremi coincidono, cioè il segmento ridotto al solo punto
è il segmento nullo, ove per segmento nullo intendiamo un qualsiasi segmento in
cui gli estremi coincidono, cioè il segmento ridotto al solo punto
 .
.
Sottomultiplo di un segmento. Il sottomultiplo secondo
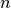 , numero naturale diverso da
, numero naturale diverso da
 , di un segmento
, di un segmento
 è un segmento
è un segmento
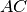 tale che
tale che
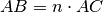 . Si può anche scrivere
. Si può anche scrivere
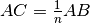 .
.
In generale il segmento
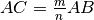 si ottiene dividendo
si ottiene dividendo
 in
in
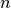 parti uguali ottenendo il segmento
parti uguali ottenendo il segmento
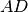 e poi sommando m segmenti congruenti ad
e poi sommando m segmenti congruenti ad
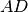 .
.
Il segmento
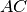 è congruente a
è congruente a
 di
di
 , cioè
, cioè
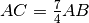 , infatti
, infatti
 è stato diviso in
è stato diviso in
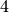 parti uguali e
parti uguali e
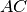 è costituito da
è costituito da
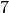 di queste parti.
di queste parti.
Punto medio. Dato un segmento
 esiste uno e uno solo punto
esiste uno e uno solo punto
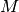 che lo divide in due parti congruenti tra di loro, questo punto si dice punto
medio del segmento.
che lo divide in due parti congruenti tra di loro, questo punto si dice punto
medio del segmento.
M è il punto medio del segmento AB in quanto
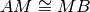 .
.
DEFINIZIONE. Si chiama punto medio di un segmento il punto interno al segmento che lo divide in due parti congruenti.
Proprietà
- somme di segmenti a due a due congruenti sono congruenti;
- differenze di segmenti a due a due congruenti sono congruenti.
Esempio
Siano
 e
e
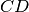 due segmenti congruenti appartenenti a una retta r che non abbiano punti in
comune. Dimostra che
due segmenti congruenti appartenenti a una retta r che non abbiano punti in
comune. Dimostra che
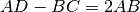
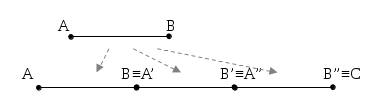
Disponiamo i punti
 ,
,
 ,
,
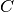 ,
,
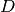 su una retta
su una retta
 come in figura.
come in figura.
Si ha che:
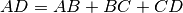 ,
,
Allora
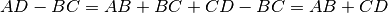
Poiché
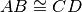 allora
allora
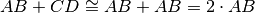
Operazioni con gli angoli¶
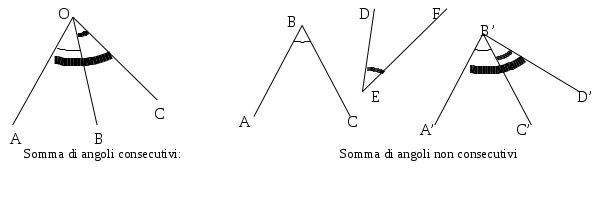
Somma di angoli. La somma di due angoli consecutivi
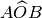 e
e
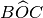 è l’angolo
è l’angolo
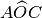 . Per sommare due angoli che non sono consecutivi, per esempio
. Per sommare due angoli che non sono consecutivi, per esempio
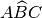 e
e
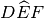 , si costruiscono due angoli consecutivi tra di loro, uno congruente a
, si costruiscono due angoli consecutivi tra di loro, uno congruente a
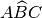 , l’altro congruente a
, l’altro congruente a
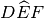 , la somma di questi due angoli consecutivi si dice anche somma dei due angoli.
, la somma di questi due angoli consecutivi si dice anche somma dei due angoli.
Differenza di angoli. Si dice differenza di due angoli, di cui il primo è maggiore o congruente al secondo, l’angolo che addizionato al secondo dà per somma il primo.
Angolo differenza
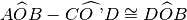 .
.
Se i due angoli sono congruenti la loro differenza è l’angolo nullo.
Multiplo di un angolo. Dato un angolo
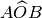 e un numero n naturale non nullo, il multiplo di
e un numero n naturale non nullo, il multiplo di
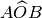 secondo
secondo
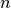 (si può scrivere
(si può scrivere
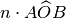 ) è l’angolo che si ottiene sommando n angoli congruenti a
) è l’angolo che si ottiene sommando n angoli congruenti a
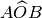 . Se
. Se
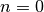 , il multiplo secondo n di qualsiasi angolo
, il multiplo secondo n di qualsiasi angolo
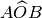 è l’angolo nullo.
è l’angolo nullo.
L’angolo
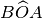 è il quadruplo di
è il quadruplo di
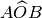 , cioè
, cioè
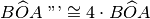
Sottomultiplo di un angolo. Il sottomultiplo secondo
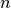 , naturale non nullo, di un angolo
, naturale non nullo, di un angolo
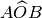 è un angolo
è un angolo
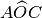 tale che
tale che
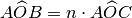 . Si può anche scrivere
. Si può anche scrivere
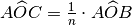 .
.
In generale un angolo
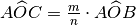 si ottiene dividendo
si ottiene dividendo
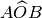 in
in
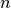 parti uguali ottenendo l’angolo
parti uguali ottenendo l’angolo
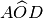 , l’angolo
, l’angolo
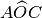 si ottiene sommando
si ottiene sommando
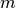 angoli
angoli
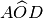 .
.
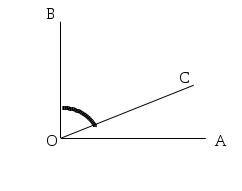
DEFINIZIONE. Si dice bisettrice di un angolo la semiretta che ha origine nel vertice dell’angolo e divide l’angolo in due angoli congruenti.
la semiretta
 di origine
di origine
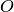 è la bisettrice dell’angolo
è la bisettrice dell’angolo
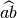 , gli angoli
, gli angoli
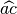 e
e
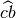 sono congruenti.
sono congruenti.
Angoli particolari¶
Possiamo ora dare dei nomi ai seguenti angoli particolari.
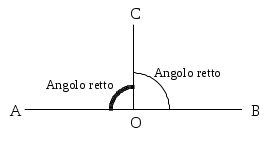
- Si dice angolo retto la metà di un angolo piatto.
- Due angoli si dicono angoli complementari se la loro somma è un angolo retto.
- Due angoli si dicono angoli supplementari se la loro somma è un angolo piatto.
- Due angoli si dicono angoli esplementari se la loro somma è un angolo giro.
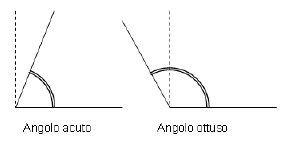
- Un angolo si dice angolo acuto se è minore di un angolo retto.
- Un angolo convesso si dice** angolo ottuso** se è maggiore di un angolo retto.
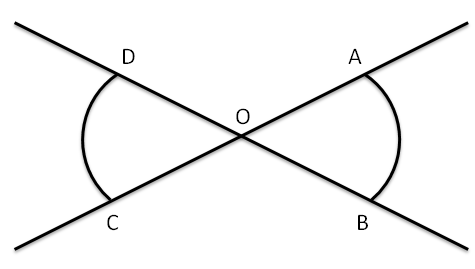
TEOREMA. Angoli opposti al vertice sono congruenti.
Ipotesi:
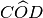 è opposto al vertice di
è opposto al vertice di
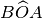
Tesi:
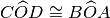
Dimostrazione:
Gli angoli
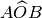 e
e
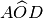 sono angoli adiacenti dato che hanno un lato in comune e gli altri due lati sono
l’uno il prolungamento dell’altro. Ma anche gli angoli
sono angoli adiacenti dato che hanno un lato in comune e gli altri due lati sono
l’uno il prolungamento dell’altro. Ma anche gli angoli
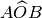 e
e
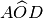 sono angoli adiacenti per lo stesso motivo. Quindi gli angoli
sono angoli adiacenti per lo stesso motivo. Quindi gli angoli
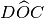 e
e
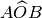 sono adiacenti allo stesso angolo
sono adiacenti allo stesso angolo
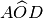 .
.
Indicando con
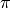 l’angolo piatto si ha:
l’angolo piatto si ha:
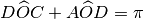 da cui
da cui
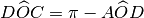 . Analogamente
. Analogamente
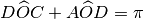 da cui
da cui
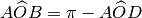 . Ne consegue che
. Ne consegue che
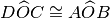 e cioè la tesi.
e cioè la tesi.
Prova tu a dimostrare il seguente teorema:
TEOREMA. Angoli supplementari di angoli congruenti sono congruenti.
Dopo aver realizzato il disegno, esplicita ipotesi e tesi. Segui poi il ragionamento del teorema precedente: se due angolo sono supplementari la loro somma è un angolo piatto...
Perpendicolari e altre definizioni
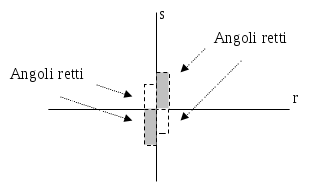
DEFINIZIONE. Due rette si dicono perpendicolari se sono incidenti e formano quattro angoli retti.
Le rette r e s sono perpendicolari, incontrandosi formano quattro angoli retti.
Per indicare che le due rette
 e
e
 sono perpendicolari si usa il simbolo
sono perpendicolari si usa il simbolo
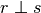 .
.
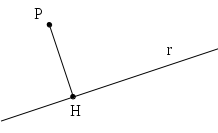
DEFINIZIONE. Si dice distanza di un punto da una retta il segmento di perpendicolare condotta dal punto alla retta.
Il segmento
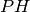 , appartenente alla perpendicolare a
, appartenente alla perpendicolare a
 passante per
passante per
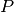 , è la distanza di
, è la distanza di
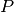 dalla retta
dalla retta
 .
.
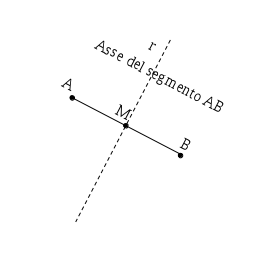
DEFINIZIONE. Si dice asse di un segmento la retta perpendicolare al segmento e passante per il punto medio del segmento.
La retta
 è l’asse del segmento
è l’asse del segmento
 in quanto è perpendicolare alla retta per
in quanto è perpendicolare alla retta per
 e passa per il punto medio di
e passa per il punto medio di
 .
.
DEFINIZIONE. Due punti si dicono** punti simmetrici rispetto a una retta** se la retta è asse del segmento che ha per estremi i due punti.
Nella figura precedente, i punti
 e
e
 sono simmetrici rispetto alla retta
sono simmetrici rispetto alla retta
 .
.
Esercizi¶
Vero o falso?
- Per un punto passa una sola retta.. tabVF
- Per due punti passa una sola retta.. tabVF
- Per tre punti passano almeno tre rette.. tabVF
- Due punti distinti del piano individuano sempre un segmento.. tabVF
- Due rette distinte del piano hanno al più un punto in comune.. tabVF
- Tre punti distinti del piano individuano almeno tre rette.. tabVF
- Due semirette distinte del piano che hanno la stessa origine sono opposte.. tabVF
- Alcuni segmenti consecutivi non sono adiacenti.. tabVF
- Due angoli che hanno il vertice in comune sono consecutivi.. tabVF
- Per un punto del piano passano solo due rette.. tabVF
- Due segmenti posti sulla stessa retta sono adiacenti.. tabVF
- Due segmenti consecutivi hanno in comune un estremo e nessun altro punto.. tabVF
Due segmenti si dicono adiacenti se:
- appartengono alla stessa retta
- sono consecutivi ma non appartengono alla stessa retta
- non sono consecutivi e appartengono alla stessa retta
- sono consecutivi e appartengono alla stessa retta
- appartengono alla stessa retta e hanno gli estremi coincidenti
Un angolo è convesso se:
- è adiacente ad un altro angolo
- i suoi lati sono rette incidenti
- contiene il prolungamento dei suoi lati
- è consecutivo ad un altro angolo
- non contiene il prolungamento dei suoi lati
Due angoli si dicono opposti al vertice se:
- sono sullo stesso piano
- sono uno concavo e uno convesso
- se hanno il vertice in comune
- se i lati dell’uno sono contenuti nell’altro
- se i lati dell’uno sono il prolungamento dei lati dell’altro
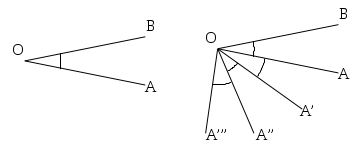
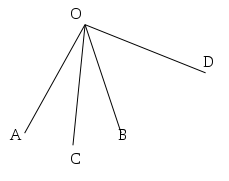
Quanti angoli individuano tre semirette aventi la stessa origine? Fai un disegno.
Rispondi a voce
- Dai la definizione di angolo.
- Qual è la differenza tra angolo piatto e angolo nullo? Fai riferimento alle definizioni e non al fatto che il primo misura 360° e il secondo 0°.
- Qual è la differenza tra angoli consecutivi e angoli adiacenti?
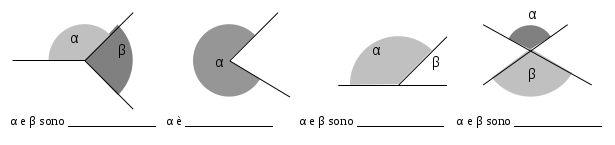
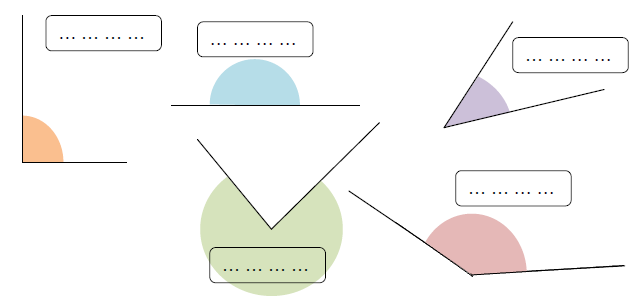
Per ciascuna figura scrivi di che angolo si tratta relativamente agli angoli colorati in grigio, scegliendo i termini tra: angolo concavo, angoli adiacenti, angoli consecutivi, angoli opposti al vertice.
Rappresenta graficamente ciascuna delle seguenti situazioni:
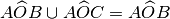
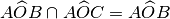
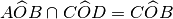
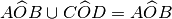
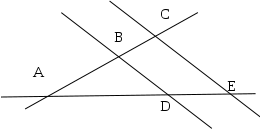
Nella figura a fianco indica
- Una coppia di segmenti consecutivi … …
- Una coppia di segmenti adiacenti … …
- Una coppia di rette incidenti … …
- Una coppia di rette parallele … …
- Una coppia di angoli consecutivi … … … …
- Una coppia di angoli adiacenti … … … …
- Una coppia di angoli opposti al vertice … … … ….
- Un angolo concavo … …
- Un angolo convesso … …
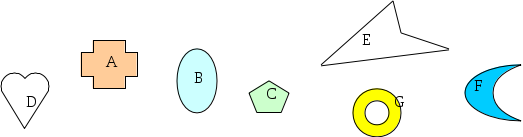
Sono convesse le figure
- [ ] A, B, C, G
- [ ] D, C, B, F
- [ ] B, C, D
- [ ] B, C
- [ ] D, E, F, G
Scrivi per esteso in italiano quanto è indicato in simboli e rappresenta con un disegno tutti i casi possibili:
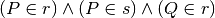 .
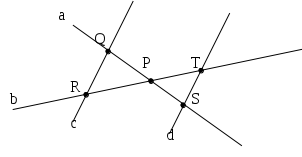
.Descrivi la costruzione della seguente figura, dove le rette c e d sono parallele
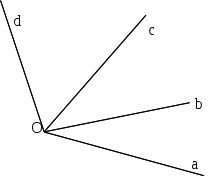
Siano a, b, c, d quattro semirette aventi l’origine in comune O disposte in ordine antiorario come in figura. Individua aiutandoti con il disegno quali sono gli angoli che si ottengono dalle seguenti operazioni:
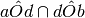
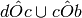
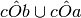
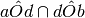
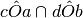
Se P è centro di un fascio di rette e A è un punto dello stesso piano, è vero che “Nel fascio di centro P esiste una retta passante per A”?
Motiva la verità o la falsità della proposizione: “Tutte le rette incidenti formano 2 coppie di angoli opposti al vertice”.
Disegna una retta a e una retta b che si incontrano in un punto X, disegna anche una retta* c* che incontra la a in Y e la b in Z. Elenca tutte le semirette e tutti i segmenti che si vengono a formare.
Disegna due rette a e b parallele tra di loro; disegna poi la retta c che interseca la* a* in A e la b in B; disegna poi la retta d che interseca a in A e b in C. Quali segmenti si vengono a formare?
Rappresenta graficamente ciascuna delle seguenti situazioni:
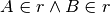 ,
,
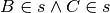 ,
,
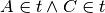
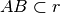 ,
,
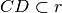 ,
,
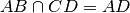 ,
,
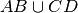 = . . . . . . . . . . . . ?
= . . . . . . . . . . . . ?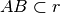 ,
,
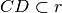 ,
,
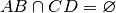 .
.
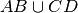 = . . . . . . . . . . . . ?
= . . . . . . . . . . . . ?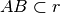 ,
,
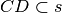 ,
,
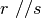 ,
,
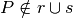
Attribuisci il nome corretto a ciascuna coppia di segmenti: adiacenti, incidenti, disgiunti, consecutivi:
Su una retta r disegna i punti A e B, sapendo che A precede B, disegna i punti C e D sapendo che D è compreso tra A e B e C segue B. Indica tutti i segmenti che si vengono a formare.
Dati cinque punti nel piano, in modo che a tre a tre non siano allineati, quante rette passanti per due di questi punti è possibile tracciare? Completa il disegno. Sai esprimere il legame generale tra il numero N di punti e il numero di rette che si possono tracciare?
Completa la frase:Quando si parla di angolo acuto o di angolo ottuso, bisogna saper eseguire l’operazione di ............................. tra angoli e aver dato la definizione di ..……….............
Due angoli sono complementari e uno è doppio dell’altro. Quale delle seguenti affermazioni è vera?
- [ ] uno è retto e l’altro è piatto
- [ ] uno è 1/3 dell’angolo retto e l’altro i 2/3 dell’angolo retto
- [ ] uno è 1/3 dell’angolo retto e l’altro 1/6 dell’angolo retto .. tab
- [ ] uno è 1/2 dell’angolo retto e l’altro è retto
- [ ] uno è 2/3 dell’angolo retto e l’altro i 4/6 dell’angolo retto
Siano α e β due angoli consecutivi esplementari e siano a e b le loro bisettrici. L’angolo tra a e b è
[ ] Piatto[ ] Retto[ ] Nullo[ ] Non si può sapere
Se α e β sono due angoli di vertice O, consecutivi e complementari e a e b le loro bisettrici, allora per l’angolo
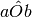 si può dire che:
si può dire che:- [ ] è uguale all’angolo retto
- [ ] è la terza parte di un angolo retto
- [ ] è la metà di un angolo retto
- [ ] è la quarta parte di un angolo retto
- [ ] non è possibile determinarne l’ampiezza
Le bisettrici di due angoli adiacenti:
- [ ] sono parallele
- [ ] sono lati di un angolo retto
- [ ] sono lati di un angolo concavo
- [ ] coincidono
- [ ] sono semirette opposte
Due angoli si dicono complementari quando:
- [ ] sono consecutivi
- [ ] sono angoli opposti al vertice
- [ ] la loro somma è un angolo retto
- [ ] ciascuno di essi è acuto
- [ ] ciascuno è la metà di un angolo retto
Dati due segmenti adiacenti AB e BC tali che
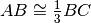 , allora per
, allora per
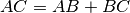 si può dire:
si può dire:- [ ]
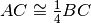
- [ ]
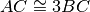
- [ ]
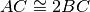
- [ ]
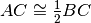
- [ ]
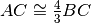
- [ ]
Due segmenti AB e CD appartengono alla stessa retta e hanno lo stesso punto medio. Si può affermare:
- [ ]
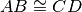
- [ ]
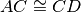
- [ ]
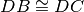
- [ ]
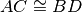
- [ ]
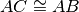
- [ ]
Per ciascuna delle affermazioni seguenti, dire se è vera o falsa, e spiegare perché
- l’angolo retto è la metà dell’angolo giro.. tabV F
- ogni angolo convesso ha due bisettrici.. tabV F
- due angoli che hanno in comune il vertice sono consecutivi.. tabV F
- un angolo ottuso è maggiore di qualunque angolo acuto.. tabV F
- sommando due angoli acuti si può ottenere un angolo piatto.. tabV F
Tre semirette a, b, c uscenti da uno stesso punto dividono il piano in tre angoli congruenti. Dopo aver rappresentato le semirette, traccia la semiretta b1 opposta di b. Allora:
- [ ] b1 è perpendicolare alla semiretta a
- [ ] b1 è bisettrice dell’angolo formato da a e c
- [ ] b1 è perpendicolare alla semiretta c
Dato l’angolo acuto
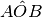 , sia OC la sua bisettrice. Sia poi OD una semiretta esterna all’angolo
come in figura, quale relazione è vera?
, sia OC la sua bisettrice. Sia poi OD una semiretta esterna all’angolo
come in figura, quale relazione è vera?- [ ]
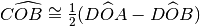
- [ ]
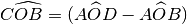
- [ ]
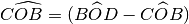
- [ ]
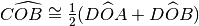
- [ ]
Individua tra i seguenti angoli quello piatto, retto, acuto, ottuso, concavo, scrivi nelle etichette il relativo nome. Per ciascuno di essi traccia la bisettrice.
Vero/Falso
- Sommando due angoli acuti si ottiene sempre un angolo acuto.. tabVF
- Sommando due angoli piatti si ottiene un angolo giro.. tabVF
- Sommando un angolo acuto e uno retto si ottiene un angolo ottuso.. tabVF
- Sommando due angoli retti si ottiene un angolo giro.. tabVF
- Sommando un angolo piatto e un angolo acuto si ottiene un angolo concavo.. tabVF
- Sommando due angoli convessi si ottiene sempre un angolo convesso.. tabVF
- Sommando un angolo retto e un angolo piatto si ottiene un angolo giro.. tabVF
Individua l’angolo:
- La differenza tra un angolo piatto è un angolo retto è un angolo ………………
- La differenza tra un angolo giro e un angolo piatto è un angolo ………………
- La differenza tra un angolo acuto e un angolo retto è un angolo ………………
- La differenza tra un angolo giro e un angolo piatto è un angolo ………………
- Il doppio di un angolo piatto è un angolo ………………
- Il doppio di un angolo retto è un angolo………………
Spiega perché se due angoli sono complementari i loro doppi sono supplementari.
Verifica, aiutandoti con un disegno, che se
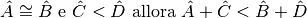 .
.Dati quattro segmenti AB>BC>CD>DE. Verifica, aiutandoti con dei disegni, che:
- AB-CD > BC-CD
- AB+DE>BC+CD
Un angolo α è retto e un angolo β è la sesta parte di un angolo piatto. A quale frazione di angolo retto corrisponde la somma α+β?
Disegnare due angoli consecutivi α e β, disegnale l’angolo γ adiacente a α non contenente β e l’angolo δ adiacente a β non contenente α. Gli angoli γ+δ e α+β sono:
[ ] complementari.. tab[ ] supplementari.. tab[ ] opposti al vertice.. tab[ ] esplementari