La misura¶
Misura di segmenti¶
Riprendiamo alcune definizioni sui segmenti:
Si dice segmento di estremi
 e
e
 (o brevemente segmento
(o brevemente segmento
 ) l’insieme dei punti
) l’insieme dei punti
 e
e
 e di tutti quelli che stanno tra
e di tutti quelli che stanno tra
 e
e
 .
.
Due segmenti
 e
e
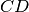 si dicono congruenti se esiste un movimento rigido che porta a coincidere
si dicono congruenti se esiste un movimento rigido che porta a coincidere
 con
con
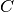 e
e
 con
con
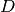 , oppure
, oppure
 con
con
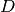 e
e
 con
con
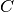 .Ricordiamo che se esiste un movimento rigido che porta a coincidere
.Ricordiamo che se esiste un movimento rigido che porta a coincidere
 con
con
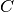 e
e
 con
con
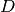 allora esiste anche un movimento rigido che porta a coincidere
allora esiste anche un movimento rigido che porta a coincidere
 con
con
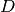 e
e
 con
con
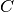 , e viceversa. È altresì vero che, anche nel caso in cui i due segmenti
appartengano alla stessa retta, uno dei due movimenti comporta il
“ribaltamento” di uno dei due segmenti che gli fa occupare posizioni al di
fuori della retta che lo contiene.
, e viceversa. È altresì vero che, anche nel caso in cui i due segmenti
appartengano alla stessa retta, uno dei due movimenti comporta il
“ribaltamento” di uno dei due segmenti che gli fa occupare posizioni al di
fuori della retta che lo contiene.
Si dice lunghezza di un segmento
 l’insieme di tutti i segmenti congruenti ad
l’insieme di tutti i segmenti congruenti ad
 .
.
Si dice distanza tra due punti
 e
e
 il segmento
il segmento
 di estremi
di estremi
 e
e
 .
.
Diamo ora una definizione particolarmente importante per l’applicazione del calcolo numerico alla geometria: la definizione di misura. Ricordiamo che la nozione di misura è alla base delle applicazioni del calcolo matematico non solo alla geometria ma anche alla fisica e alla tecnologia in generale. Il processo di misurazione è analogo a tutti i campi di applicazioni: si tratta di trovare un modo per assegnare a una grandezza un numero. Questo numero si ottiene confrontando due grandezze dello stesso tipo. Per esempio, per misurare la massa di un oggetto si confronta la sua massa con quella di un oggetto campione, di solito un oggetto di 1 kg.
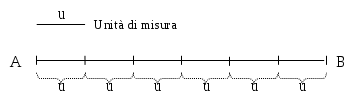
Per misurare un segmento
 si confronta questo segmento con un altro segmento scelto come unità di
misura, di solito indicato con
si confronta questo segmento con un altro segmento scelto come unità di
misura, di solito indicato con
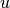 .
.
Nel confronto tra il segmento
 e il segmento
e il segmento
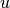 , possono verificarsi i tre casi seguenti:
, possono verificarsi i tre casi seguenti:
1. Il segmento
 è multiplo del segmento
è multiplo del segmento
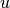 secondo il numero naturale
secondo il numero naturale
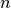 , precisamente
, precisamente
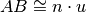 . In questo caso la misura di
. In questo caso la misura di
 rispetto a
rispetto a
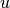 è il numero naturale
è il numero naturale
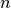 . Si scrive
. Si scrive
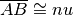
Il segmento
 misura
misura
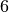 rispetto all’unità di misura
rispetto all’unità di misura
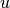 , in quanto
, in quanto
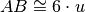 .
.
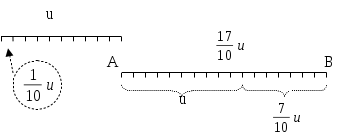
2. Il segmento
 non è un multiplo intero di u ma è un multiplo di un sottomultiplo di
non è un multiplo intero di u ma è un multiplo di un sottomultiplo di
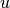 , precisamente
, precisamente
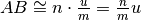 . In questo caso la misura di
. In questo caso la misura di
 rispetto a
rispetto a
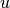 è il numero razionale
è il numero razionale
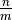 . Si scrive
. Si scrive
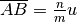 .
.
Il segmento AB è congruente a 17 volte il segmento
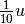 , quindi AB misura
, quindi AB misura
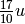 .
.
3. Il segmento
 non è un multiplo né di
non è un multiplo né di
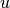 né di nessun sottomultiplo di
né di nessun sottomultiplo di
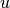 . In questo caso si dice che
. In questo caso si dice che
 e
e
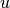 sono incommensurabili, nei casi precedenti si dice che sono commensurabili.
Anche in questo caso è
possibile attribuire ad
sono incommensurabili, nei casi precedenti si dice che sono commensurabili.
Anche in questo caso è
possibile attribuire ad
 un numero che ne esprime la misura rispetto a
un numero che ne esprime la misura rispetto a
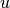 , si tratta però di un numero irrazionale. La complessità dell’argomento
richiede alcune conoscenze più avanzate di matematica, pertanto la tematica
della misura delle grandezze
incommensurabili sarà approfondita nel seguito. Qui ci accontentiamo di
accennare al caso storicamente più noto di segmenti incommensurabili: la
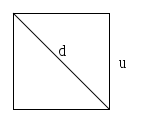
diagonale di un quadrato misurata rispetto al suo lato.
, si tratta però di un numero irrazionale. La complessità dell’argomento
richiede alcune conoscenze più avanzate di matematica, pertanto la tematica
della misura delle grandezze
incommensurabili sarà approfondita nel seguito. Qui ci accontentiamo di
accennare al caso storicamente più noto di segmenti incommensurabili: la
diagonale di un quadrato misurata rispetto al suo lato.
Prendendo come unità di misura il lato di un quadrato la sua diagonale è
incommensurabile con il lato stesso. Applicando il teorema di Pitagora,
ricorderai infatti che
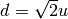 e che
e che
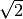 è un numero irrazionale.
è un numero irrazionale.
Proponiamo una dimostrazione dell’irrazionalità del numero
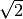 utilizzando il metodo della dimostrazione per assurdo.
utilizzando il metodo della dimostrazione per assurdo.
TEOREMA.
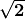 è un numero irrazionale.
è un numero irrazionale.
Dimostrazione: supponiamo per assurdo che
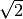 sia un numero razionale, cioè che sia possibile scrivere
sia un numero razionale, cioè che sia possibile scrivere
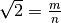 , con
, con
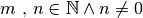 . Allora, per definizione di radice quadrata, si avrebbe
. Allora, per definizione di radice quadrata, si avrebbe
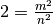 , da cui
, da cui
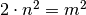 . I due membri dovrebbero quindi rappresentare lo stesso numero naturale (il
teorema fondamentale dell’Aritmetica assicura l’unicità della scomposizione
in fattori primi). Essendo
. I due membri dovrebbero quindi rappresentare lo stesso numero naturale (il
teorema fondamentale dell’Aritmetica assicura l’unicità della scomposizione
in fattori primi). Essendo
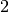 un numero primo, dovrebbe comparire come fattore sia al primo sia al secondo
membro lo stesso numero di volte. Inoltre
un numero primo, dovrebbe comparire come fattore sia al primo sia al secondo
membro lo stesso numero di volte. Inoltre
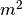 ed
ed
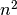 o sono dispari e quindi non contengono
o sono dispari e quindi non contengono
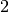 come fattore, oppure se contengono il fattore
come fattore, oppure se contengono il fattore
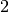 , lo contengono un numero pari di volte (vediamo qualche esempio
, lo contengono un numero pari di volte (vediamo qualche esempio
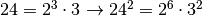 ,
,
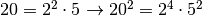 ). Ma
). Ma
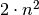 contiene il fattore
contiene il fattore
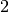 un numero dispari di volte, mentre *m*2 lo contiene un numero pari di volte.
Pertanto l’uguaglianza
un numero dispari di volte, mentre *m*2 lo contiene un numero pari di volte.
Pertanto l’uguaglianza
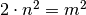 non può essere mai verificata; l’assurdo dipende dall’aver supposto
non può essere mai verificata; l’assurdo dipende dall’aver supposto
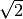 razionale. q.e.d.
razionale. q.e.d.
Un altro esempio di numero irrazionale, e di conseguenza di due “lunghezze”
incommensurabili, è
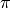 , che rappresenta il rapporto tra la misura della lunghezza ‘rettificata’ di
una qualsiasi circonferenza e la misura della lunghezza del suo diametro.
, che rappresenta il rapporto tra la misura della lunghezza ‘rettificata’ di
una qualsiasi circonferenza e la misura della lunghezza del suo diametro.
In generale, dato un segmento
 e un segmento
e un segmento
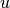 , preso come unità di misura, esiste sempre un numero reale positivo che
esprime la misura di
, preso come unità di misura, esiste sempre un numero reale positivo che
esprime la misura di
 rispetto a
rispetto a
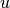 . Questo numero è unico, ossia ogni segmento ha una sola misura. Viceversa,
dato un qualsiasi numero
. Questo numero è unico, ossia ogni segmento ha una sola misura. Viceversa,
dato un qualsiasi numero
 reale positivo e un segmento
reale positivo e un segmento
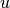 , preso come unità di misura, è sempre possibile costruire un segmento che
misura esattamente
, preso come unità di misura, è sempre possibile costruire un segmento che
misura esattamente
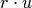 rispetto all’unità di misura fissata.
rispetto all’unità di misura fissata.
Osservazioni
- Se due segmenti sono congruenti, le loro misure, rispetto alla stessa unità
di misura, sono uguali:
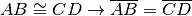 .
. - La misura di un segmento
 somma di due segmenti
somma di due segmenti
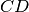 e
e
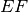 , cioè
, cioè
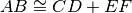 è uguale alla somma delle misure di
è uguale alla somma delle misure di
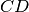 e
e
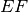 :
:
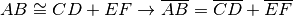 .
. - La misura di un segmento multiplo secondo n del segmento
 è uguale al prodotto di
è uguale al prodotto di
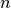 per la misura di
per la misura di
 :
:
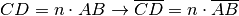 .
. - Definito il rapporto tra due segmenti come il quoziente tra le loro misure
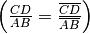 , rispetto alla stessa unità di misura, si ha che il rapporto non dipende
dall’unità di misura usata per misurare i segmenti, cioè il numero che si
ottiene è sempre lo stesso indipendentemente dall’unità scelta per
misurare.
, rispetto alla stessa unità di misura, si ha che il rapporto non dipende
dall’unità di misura usata per misurare i segmenti, cioè il numero che si
ottiene è sempre lo stesso indipendentemente dall’unità scelta per
misurare.
Possiamo pertanto parlare di misura della lunghezza di un segmento e darne la seguente definizione generale.
DEFINIZIONE. Dato un segmento
 e un segmento
e un segmento
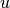 , preso come unità di misura, si dice misura della lunghezza del segmento
, preso come unità di misura, si dice misura della lunghezza del segmento
 il numero reale positivo
il numero reale positivo
 per il quale
per il quale
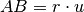 .
.
Nella realtà fisica per misurare la lunghezza degli oggetti reali (l’altezza
di una persona, la lunghezza di un banco, di una stanza, di un terreno…) si
usa come unità di misura il metro, indicato con
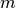 , con i suoi multipli (decametro, ettometro, chilometro…) e i suoi
sottomultipli (decimetro, centimetro, millimetro…). Anche nella geometria, che
tratta di segmenti ideali non riscontrabili perfettamente nella realtà, si usa
come unità di misura un segmento di un metro.
, con i suoi multipli (decametro, ettometro, chilometro…) e i suoi
sottomultipli (decimetro, centimetro, millimetro…). Anche nella geometria, che
tratta di segmenti ideali non riscontrabili perfettamente nella realtà, si usa
come unità di misura un segmento di un metro.
Riassumendo, ricordiamo simboli e nozioni che riguardano due punti
 e
e
 .
.
- I due punti presi singolarmente, che con notazione insiemistica si indica
con
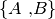 .
. - La retta passante per i due punti, che si indica con il simbolo
 oppure
oppure
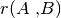 .
. - La semiretta di origine
 e passante per
e passante per
 , che si indica con il simbolo
, che si indica con il simbolo
 oppure
oppure
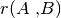 .
. - Il segmento di estremi
 e
e
 , che si indica con il simbolo
, che si indica con il simbolo
 .
. - La distanza tra i punti
 e
e
 , cioè il segmento
, cioè il segmento
 , che si indica con il simbolo
, che si indica con il simbolo
 oppure
oppure
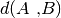 .
. - La lunghezza del segmento
 , cioè l’insieme di tutti i segmenti congruenti ad
, cioè l’insieme di tutti i segmenti congruenti ad
 , che si indica con il simbolo
, che si indica con il simbolo
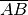 .
. - La misura della lunghezza del segmento
 rispetto a una fissata unità di misura, che si indica con il simbolo
rispetto a una fissata unità di misura, che si indica con il simbolo
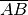 .
. - La misura della distanza tra i punti
 e
e
 , che corrisponde alla misura del segmento
, che corrisponde alla misura del segmento
 e si indica con il simbolo
e si indica con il simbolo
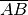 .
.
Tutte queste distinzioni sono importanti dal punto di vista
dell’organizzazione teorica delle geometria, tuttavia dal punto di vista
applicativo e della quotidianità del linguaggio geometrico possono risultare
pedanti e noiose, spesso si usano espressione più generiche, finché si
riescono ad evitare possibili malintesi. Sebbene a rigore si dovrebbe dire “La
misura della lunghezza del segmento
 rispetto al centimetro è
rispetto al centimetro è
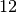 ” molto spesso si usa dire “Il segmento
” molto spesso si usa dire “Il segmento
 è lungo
è lungo
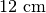 ” oppure “
” oppure “
 misura
misura
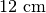 ” o ancora “La distanza
” o ancora “La distanza
 è lunga
è lunga
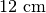 ” o più semplicemente “Un segmento di
” o più semplicemente “Un segmento di
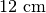 ” ecc.
” ecc.
Misura degli angoli¶
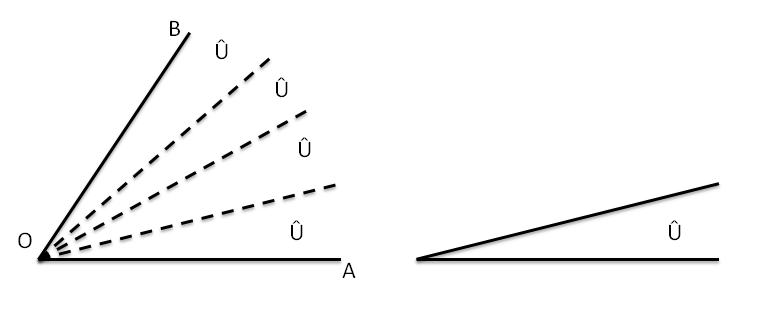
Il procedimento che si usa per misurare gli angoli è del tutto analogo a quello
usato per misurare i segmenti. Si fissa una unità di misura, cioè un angolo
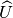 , e si confronta l’angolo da misurare con l’angolo
, e si confronta l’angolo da misurare con l’angolo
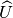 . Come risultato si avrà un numero reale positivo che chiamiamo misura
dell’ampiezza dell’angolo.
. Come risultato si avrà un numero reale positivo che chiamiamo misura
dell’ampiezza dell’angolo.
L’angolo
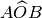 è quattro volte l’angolo
è quattro volte l’angolo
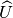 , pertanto
, pertanto
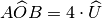
Per misurare gli angoli l’unità di misura comunemente usata è la trecentosessantesima parte dell’angolo giro, quest’angolo si chiama grado, e si indica con un cerchietto posto in alto °. Si ha quindi, usando come unità di misura il grado, che:
l’angolo retto misura
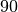 gradi, si scrive
gradi, si scrive
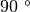 ;
;
l’angolo piatto misura
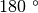
- l’angolo giro misura
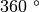 .
.
I sottomultipli del grado sono il primo che è la sessantesima parte di un grado
(in simboli
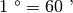 ) e il secondo che è la sessantesima parte del primo (in simboli
) e il secondo che è la sessantesima parte del primo (in simboli
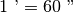 ) e quindi la tremilaseicentesima parte del grado (in simboli
) e quindi la tremilaseicentesima parte del grado (in simboli
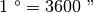 ).
).
Esempio
- Calcola la misura in gradi del supplementare dell’angolo che misura * :math:`35 text{ °} 15 text{ ‘} 40 text{ ‘’}` *.
Occorre eseguire la sottrazione
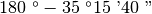 . Per eseguire praticamente questa sottrazione si trasforma
. Per eseguire praticamente questa sottrazione si trasforma
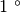 in
in
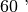 e
e
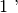 in
in
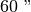 , precisamente si scrive
, precisamente si scrive
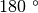 come
come
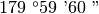 , pertanto:
, pertanto:
179°59‘60”-
35°15‘40”=
144°44‘20”
Quindi
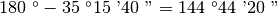 .
.
Il sistema di misura degli angoli che abbiamo illustrato prende il nome di sistema sessagesimale. Spesso, però, per praticità, anziché usare i primi, i secondi e i decimi di secondo, si usano i decimi di grado: in questo caso il sistema si dice sistema sessadecimale.
In base a quanto abbiamo illustrato, vediamo brevemente come si passa da un sistema all’altro.
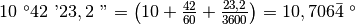 ,
,
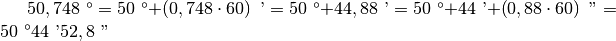 .
.
I sistemi sessagesimale e sessadecimale non sono gli unici usati per le misure degli angoli.
Osservando i tasti di una calcolatrice scientifica, si può vedere che ci sono tre sistemi principali le cui unità sono rispettivamente il grado sessagesimale (DEG), il grado centesimale (GRAD) e il radiante (RAD).
Il grado centesimale è importante per gli strumenti tecnici. Si può passare
dal grado sessagesimale al grado centesimale e viceversa con una semplice
proporzione, sapendo che l’angolo retto, pari a
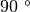 , corrisponde a 100 gradi centesimali (in simboli
, corrisponde a 100 gradi centesimali (in simboli
 ).
).
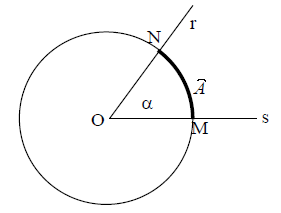
Il radiante è utile nello studio della trigonometria e dell’analisi
matematica. L’angolo di misura 1 radiante (in simboli 1 rad) è congruente
ad un angolo con vertice nel centro di una circonferenza e tale
che la misura dell’arco da esso individuato è uguale alla misura del raggio
della circonferenza stessa. Come si può facilmente intuire, il radiante ed il
grado sono grandezze incommensurabili. Facendo riferimento alla figura,
l’angolo α formato dalla semiretta
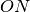 e
e
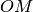 misura 1 radiante se l’arco
misura 1 radiante se l’arco
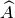 misura quanto il raggio della circonferenza.
misura quanto il raggio della circonferenza.
La misura di un arco va fatta con una modalità differente rispetto a quella
utilizzata per la misura dei segmenti. Si può immaginare di utilizzare come
strumento di misura un metro flessibile, ovvero un filo flessibile ma
inestensibile, che si può piegare ma non si può
allungare o accorciare, su cui siano state tracciate a distanza regolare delle
tacche corrispondenti a sottomultipli dell’unità di misura delle lunghezze;
una di queste tacche viene assunta come origine del metro. Facendo combaciare
l’origine del metro flessibile con il punto
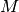 e flettendo il metro in modo che si sovrapponga all’arco
e flettendo il metro in modo che si sovrapponga all’arco
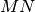 si otterrà la lunghezza dell’arco
si otterrà la lunghezza dell’arco
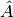 . Ricordando che il rapporto tra la misura della circonferenza ed il raggio vale
. Ricordando che il rapporto tra la misura della circonferenza ed il raggio vale
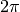 , dove
, dove
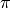 è il numero irrazionale
è il numero irrazionale
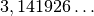 (i puntini indicano che la parte decimale è infinita e non periodica),
possiamo intuire che il valore dell’angolo giro (
(i puntini indicano che la parte decimale è infinita e non periodica),
possiamo intuire che il valore dell’angolo giro (
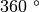 ), corrispondente ad un arco che coincide con l’intera circonferenza, vale
), corrispondente ad un arco che coincide con l’intera circonferenza, vale
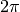 radianti.
radianti.
Diamo ora una tabella che fornisce i valori degli angoli più comuni espressi in radianti:
| angolo in gradi | angolo in radianti |
| 360° | 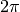 |
| 180° | 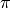 |
| 90° | 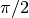 |
| 60° | 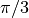 |
| 30° | 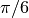 |
| 45° | 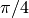 |
| 270° | 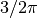 |
Angoli negativi¶
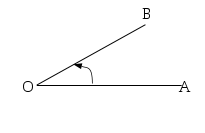
Nei paragrafi precedenti abbiamo definito l’angolo come l’insieme dei punti compresi tra due semirette aventi la stessa origine O. Possiamo però definire l’angolo anche come rotazione di una semiretta intorno alla propria origine, la misura di un angolo diventa allora la misura dell’entità della rotazione.
L’angolo può essere definito come rotazione di una semiretta intorno alla sua origine.
Dal momento che una rotazione può essere effettuata in due versi, orario od antiorario, si assume uno dei due versi di rotazione come positivo e l’altro negativo. Per motivi storici si è assunto come positivo il verso di rotazione antiorario e negativo quello orario.
Da questa definizione segue che
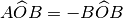 , dove
, dove
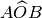 è l’angolo formato dalla semiretta
è l’angolo formato dalla semiretta
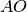 rispetto alla semiretta
rispetto alla semiretta
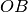 .
.
Inoltre la misura dell’angolo è definita a meno di un multiplo intero di
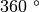 , ovvero gli angoli
, ovvero gli angoli
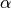 e
e
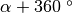 hanno la stessa ampiezza, lo stesso dicasi per tutti gli angoli del tipo
hanno la stessa ampiezza, lo stesso dicasi per tutti gli angoli del tipo
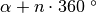 o
o
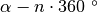 con n intero. Per esempio, sono congruenti gli angoli di
con n intero. Per esempio, sono congruenti gli angoli di
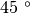 , di
, di
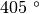 ,
,
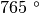 ,…
,…
Esercizi¶
Due segmenti adiacenti AB e BC misurano rispettivamente 12cm e 15cm, calcola la misura della distanza tra i loro punti medi M e N.
Dati due segmenti AB e CD, con
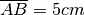 e
e
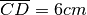 , sottrai dalla loro somma la loro differenza e verifica che si ottiene un
segmento congruente al doppio del segmento minore.
, sottrai dalla loro somma la loro differenza e verifica che si ottiene un
segmento congruente al doppio del segmento minore.Il triplo di un segmento AB uguaglia il quadruplo di un segmento CD; determinare il rapporto tra AB e CD.
Due segmenti AP e PB sono tali che
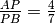 ; determina la misura del segmento
; determina la misura del segmento
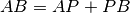 , sapendo che AP misura 16cm.
, sapendo che AP misura 16cm.I segmenti OA, AB e BC sono adiacenti; M ed N sono rispettivamente i punti medi di OA e di BC. Se
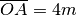 ,
,
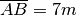 e
e
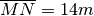 quanto misura BC?
quanto misura BC?Su una semiretta di origine O sono disposti tre punti A, B, C tali che
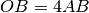 ,
,
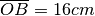 , BC supera AB di 2 cm. Determina la lunghezza di BC.
, BC supera AB di 2 cm. Determina la lunghezza di BC.Calcola la misura dell’ampiezza di due angoli di cui si sa che sono complementari e che la loro differenza misura 12°30’.
Calcola la misura di due angoli adiacenti, di cui si sa che uno è 3/4 dell’altro.
Un angolo che sia i 3/5 di un angolo giro misura:[ ] 72° [ ] 216° [ ] 330° [ ] 550°
Se ad un angolo retto sommo i suoi 5/3 ottengo un angolo la cui misura è:
[ ] 240° [ ] 150° [ ] 144° [ ] 125°
Le quattro semirette a, b, c, d hanno la stessa origine O e sono disposte in senso antiorario; m è la bisettrice sia dell’angolo
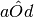 che dell’angolo b
che dell’angolo b
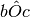 . Sapendo
. Sapendo
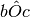 che misura 70° e
che misura 70° e
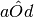 misura 110° quanto misurano gli angoli
misura 110° quanto misurano gli angoli
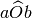 e
e
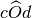 ?
?La somma di due angoli è 3/4 di un angolo retto. Sapendo che uno è doppio dell’altro quale frazione di angolo retto è ciascuno dei due angoli?
Disegna tre angoli consecutivi
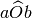 ,
,
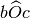 ,
,
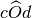 di cui si sa che la loro somma è un angolo piatto e
di cui si sa che la loro somma è un angolo piatto e
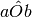 è
è
 dell’angolo piatto. Determina quanto misura l’angolo formato dalle
bisettrici degli angoli
dell’angolo piatto. Determina quanto misura l’angolo formato dalle
bisettrici degli angoli
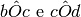 .
.Su una semiretta di origine A segna il segmento AB, il segmento BC=3AB e il segmento
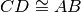 , i punti sono consecutivi secondo l’ordine alfabetico. Secondo quale
numero frazionario AD e multiplo di BC?
, i punti sono consecutivi secondo l’ordine alfabetico. Secondo quale
numero frazionario AD e multiplo di BC?Su una semiretta di origine O si hanno i segmenti OA e OB con OB>OA. Se M è il punto medio di OA e N è il punto medio di OB, quale delle due seguenti relazioni è vera?
[ ]
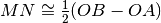 [ ]
[ ]
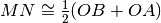
Su una semiretta di origine O si prendono i punti ABC con OC>OB>OA. Sia M il punto medio di OA e N il punto medio di BC. Quale delle seguenti relazioni è vera?
[ ]
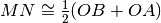 [ ]
[ ]
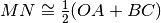 [ ]
[ ]
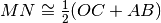
Su una retta, i punti A, B, C, D si susseguono secondo l’ordine alfabetico. Se AB è congruente a CD i punti medi di BC e AD coincidono? Sai spiegare perché?
Siano AB e CD due segmenti congruenti disposti su una retta r e non aventi alcun punto in comune. Dimostra che AC è congruente a BD.
Siano AB e CD due segmenti congruenti disposti su una retta r, non aventi alcun punto in comune e in modo che AB preceda CD. Dimostra che il punto medio di BC è anche punto medio di AD.
Siano AB e CD due segmenti congruenti adiacenti, siano M e N i rispettivi punti medi, dimostra che MN è congruente a CD.
Siano AB e CD due segmenti congruenti adiacenti tali che
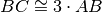 , siano M e N i rispettivi punti medi, dimostra che
, siano M e N i rispettivi punti medi, dimostra che
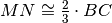 .
.Siano AB e BC due segmenti adiacenti non necessariamente congruenti, sia M il punto medio di AC ed N il punto medio di BC, dimostra che
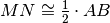 .
.* Siano AB e BC due segmenti adiacenti e congruenti; siano M e N i punti medi rispettivamente di AB e BC. Dimostrare che
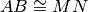 .
.* Siano AB e BC due segmenti adiacenti tali che AB < BC, e siano M e N i loro rispettivi punti medi. Dimostrare che AB < MN e che MN < BC.
In un piano gli angoli
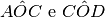 sono adiacenti. Sia OF bisettrice di
sono adiacenti. Sia OF bisettrice di
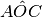 e OE bisettrice di
e OE bisettrice di
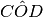 . Spiega perché
. Spiega perché
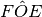 è retto.
è retto.Quattro semirette con origine nello stesso punto dividono un angolo giro in quattro angoli α, β, γ, δ disposti in senso antiorario secondo l’ordine alfabetico. Si sa che α è congruente a γ e β è congruente a δ. Dimostra che ci sono alcune semirette opposte, quali sono?
Quando due angoli sono complementari? Disegna un angolo convesso e i suoi complementari consecutivi, spiega come hai costruito gli angoli complementari. Spiega perché i complementari dello stesso angolo sono congruenti.
Sia M il punto medio del segmento AB e sia P un punto compreso tra M e B. Che relazione esiste tra MP e la differenza AP-BP? Per aiutarti costruisci il punto Q tale che
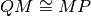 .
.Sia
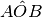 un angolo qualunque e OC la sua bisettrice. Sia OD una semiretta esterna
all’angolo
un angolo qualunque e OC la sua bisettrice. Sia OD una semiretta esterna
all’angolo
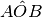 . Che relazione c’è tra
. Che relazione c’è tra
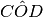 e
e
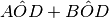 ? Per aiutarti traccia la bisettrice di
? Per aiutarti traccia la bisettrice di
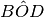 .
.Dimostra che le bisettrici di due angoli adiacenti formano un angolo retto.
Siano r e s due rette incidenti, dimostra che le bisettrici dei quattro angoli formati da r e s sono perpendicolari.
* Disegnare un angolo
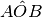 e la sua bisettrice OC, quindi disegnare un secondo angolo
e la sua bisettrice OC, quindi disegnare un secondo angolo
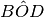 , consecutivo al primo, e la sua bisettrice OE. Dimostrare che
, consecutivo al primo, e la sua bisettrice OE. Dimostrare che
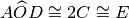 .
.* Dimostrare che le bisettrici di due angoli opposti al vertice hanno lo stesso sostegno, cioè sono
semirette opposte.
* Disegnare un angolo concavo
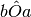 e la sua bisettrice d. Dimostrare che la semiretta opposta a d è la
bisettrice dell’angolo convesso
e la sua bisettrice d. Dimostrare che la semiretta opposta a d è la
bisettrice dell’angolo convesso
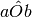 .
.* Disegnare gli angoli consecutivi
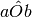 e
e
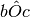 , quindi le loro rispettive bisettrici d ed e. Dimostrare che se gli angoli
, quindi le loro rispettive bisettrici d ed e. Dimostrare che se gli angoli
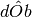 e
e
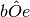 sono complementari, allora gli angoli
sono complementari, allora gli angoli
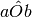 e
e
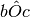 sono adiacenti.
sono adiacenti.
* Disegnare due angoli consecutivi
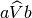 e
e
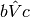 e le loro bisettrici d ed e. Supposto che le bisettrici siano perpendicolari,
dimostrare che, presi due punti qualunque rispettivamente sulle semirette a e
c, essi sono allineati con V .
e le loro bisettrici d ed e. Supposto che le bisettrici siano perpendicolari,
dimostrare che, presi due punti qualunque rispettivamente sulle semirette a e
c, essi sono allineati con V .
Gli esercizi indicati con * sono tratti da Matematica 1, Dipartimento di Matematica, ITIS V.Volterra, San Donà di Piave, Versione [11-12] [S-A11], pag. 112; licenza CC, BY-NC-BD, per gentile concessione dei prof. che hanno redatto il libro. Il libro è scaricabile da
http://www.istitutovolterra.it/dipartimenti/matematica/dipmath/docs/M1_1112.pdf